Ciencia

Postulados de Bohr

Es un placer poder comunicar el asombro que sentí cuando descubrí que la realidad era aún más compleja que como me habían contado hasta el momento, a mis tiernitos 17 años.

Yo leí la Teoría de la Relatividad de Einstein cuando tenía 16, pero creo que no la comprendí, ni mucho menos la parte matemática de la misma. Leí el Principio de Incertidumbre de Heisemberg una semana santa sacándolo de la biblioteca del Instituto de Bachillerato Mixto de Colmenar Viejo. Me estalló la cabeza.

Quería comprender y no tenía a nadie cercano que pudiese explicarme lo que había leído.

Mi profesora de química, que no sabía nada de mecánica cuántica, me remitía a Ana Cañas, que era la profesora de física que no me daba clase. Pero que tenía a bien discutir conmigo sobre la viabilidad de la existencia de partículas elementales diferentes a las que conocíamos, esos protones, esos electrones, esos neutroncillos… e intentar justificar o hacerme entender que la singularidad en las ecuaciones de Lorentz que usaba Einstein en su Relatividad Especial no aplicaba a los fotones, pues su masa en reposo no tiene sentido.

Gracias a ella quizá terminé por estudiar Química Cuántica y ver todo lo que me faltaba por ver… que siempre será inabarcable. Conocí a gente estupenda, como mi queridísimo Xabi López Pestaña, con quienes compartimos conversaciones sobre mujeres y mecánica cuántica, sobre el mar, el urbanismo, la política y los grupos de simetría.

También a Alberto Luna, que me enseñó a valorar Dune y sus gusanos, o José Luis Sanz Vicario, a quien le regalé mi querida pieza del Principio de Incertidumbre.

Este sábado pasado tuve la suerte de poder dar una clase sobre la importancia teórico-filosófica de las revoluciones físicas de la Relatividad (Especial y General) y la Mecánica Cuántica. Hablé del debate Bohr-Einstein, de la dualidad onda-corpúsculo, de la deformación del espacio, de la concepción del espacio absoluto cartesiano… los ejercicios son sencillos, pero la comprensión de la repercusión de esta revolución del conocimiento es algo que engrandece la mente hasta lugares inimaginables.

En la imagen que sirve de cabecera a este artículo está mi demostración de cómo inferir desde los postulados de Bohr las explicaciones para la fórmula de Rydberg de los espectros electromagnéticos.

Probabilidades

Siempre se me han dado mal los problemas de probabilidad, quizá (casi seguro) porque no los estudié durante el periodo de formación que más aproveché de mi vida: la adolescencia. Así que cuando me preguntan algo de este tipo me echo a temblar (con toda probabilidad). Cada año me toca volver a hojear apuntes al respecto para poder impartir las clases particulares de matemáticas que, cada vez más, incluyen más contenido de probabilidad y estadística, incluso en las matemáticas «de ciencias».

Pero lo que no me podía esperar era que un alumno de los talleres de poesía me preguntase (por si yo lo sabía) cuál era la probabilidad de que, tirando 5 tetraedros numerados del 1 al 4, saliese al menos un uno.

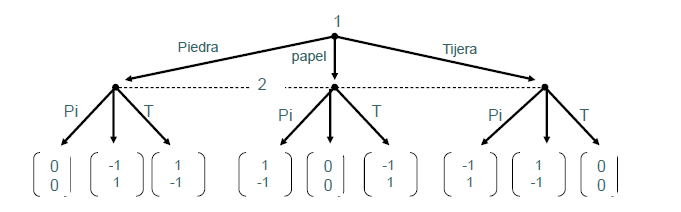
Como estaba centrado en el taller de escritura, no quise dedicarle mucho tiempo y tan sólo le dije que se podía resolver mediante diagrama de árbol (con 5 tiradas sucesivas) donde cada rama tendría un peso probabilístico del 25%. Posteriormente, le dije que podía simplificarse como un problema binario (uno 25% / no-uno 75%).

Con eso, sin mucho más, él me dijo que había realizado una simulación, donde, tras 100 millones de iteraciones, obtenía 0.76268608, es decir, aproximadamente, 76,27% de probabilidad de obtener, al menos, un uno.

No obstante, me quedé pensando que era un problema mucho más sencillo de lo que yo había estimado, si se consideraba que la probabilidad de que salga al menos un uno es equivalente al total (100%) menos la probabilidad de que no te salga un uno, es decir:

P(UNO) = P(TOTAL) – (P(NO-UNO))NumEventos = 1 – (0,75)5 = 0,7626953125 ≅ 76,27%

pero que difiere de su simulación en una diezmilésima.

Lo que más me ha interesado de esta pregunta es que resuelve muchas de mis dudas (no cuantitativamente) sobre la probabilidad de tener un accidente a lo largo de la vida o cortarse cocinando, o caerse en una caminata…

Y es que si pudiésemos cuantificar, por ejemplo, en un 99,999% la probabilidad de no caerse en un paso durante una caminata, obtendríamos que, en una ruta de unos 10.000 pasos, sería del:

P(CAERSE) = P(TOTAL) – (P(NO-CAERSE))10.000 = 1 – 0,9999910000 = 0,095163034 ≅ 9,52%

Lo que justifica, por fin, cierto miedo que le tengo a la vida, así, en general, pues es aquello que va haciendo crecer el número de eventos y, por tanto, reduciendo la probabilidad de no sufrir nunca.

De hecho, sin entrar en detalles, esta es la razón que explica el riesgo de contraer cánceres (mutaciones probables cancerígenas) y hace que no tenga demasiado en cuenta otros factores que aumentan la probabilidad de contraerlo.

Tontunas pseudomatemáticas

El otro día encontré en una red social este presunto test matemático que, carente de contexto, no está tan bien formulado como él mismo se cree: nadie ha afirmado previamente que la operación que se realiza sea constante, que se trate de una sucesión «regular» y no de unos números colocados al azar, sin embargo, nos gusta ver patrones, sentir que el mundo está ordenado, así que nos disponemos a lanzar suposiciones (no cálculos, no vaya a ser que…) y así se propone que para el 3 corresponde el 30, el 18, etc. Pero no se ofrecen muchas razones (ninguna) para las soluciones propuestas, tan solo el resultado, como si se hubieran copiado de alguien en un examen.

Yo aventuro a suponer que lo que se hace es ir restando a cada número (partiendo de 18) un par menor, es decir, 16, 14, 12… hasta que puedo realizar el cálculo (sin álgebra mediante) para obtener una solución más o menos cutre:

Pero no me quedo muy satisfecho de no haber sido más riguroso, no haber realizado un cálculo algebraico, generalizable, pues era una sucesión (recursiva) a la que se le iba restando una progresión aritmética de distancia=-2

A lo más que he llegado es a tener algo de la forma:

Sean 18, 16, 14… los términos de la progresión aritmética donde b1=18, d=-2
tenemos que bn = b1 + d·(n-1) = 18 – 2·(n-1) = 20 – 2n

Podemos definir an = an-1 – bn, siendo a1=90.

No he logrado demostrar si esta sucesión podría tener un término general independientemente de su definición recursiva, pero tampoco le quiero dedicar mucho más tiempo. Algo me dice que seguro que sí se podría y esto me reconcomerá unas horas, pero voy a dejar que ocurra.

Blancos

Soy un gran admirador de la obra divulgativa de Peter Watson, de quien he leído ávidamente su libro IDEAS sobre la historia intelectual de la humanidad y que me pareció una verdadera joya.

También me leí este verano, prestado por mi amigo Xabi, su libro Convergencias, mucho más centrado de manera casi exclusiva en la historia de la ciencia del siglo XIX y XX, así que gran parte del mismo se solapa con el que me estoy leyendo, de manera mucho más irregular que el de IDEAS, titulado Historia Intelectual del Siglo XX.

Pero a lo que quería llegar (a lo que el título de esta entrada hace referencia) es a que cada vez más me parece que es algo sesgado, especialmente en cuanto a representación de mujeres en esa historia intelectual (no es que no se mencione a Marie Curie, pero no hace especial hincapié en temas como la incorporación de la mujer al mercado laboral, por ejemplo, y muy poco a las luchas feministas) así como tampoco hay apenas historia intelectual de otros continentes que no sea Europa (la Europa caucásica y casi gérmánica), o Americana (aunque cabría decir estadounidense).

No digo con ello que los logros de las mentes de genios como Einstein, Picasso o Freud no sean reseñables, pero poco se habla de sus lados oscuros, por ejemplo, en el trato a las mujeres de sus vidas. Y no me parece baladí. ¿Podrían haber sido grandes genios si no hubiesen estado eximidos de responsabilidades paternales?

De nuevo me vuelvo a acordar de mi amigo Xabi quien dice de sí mismo con la humildad que siempre le ha caracterizado que nunca será un gran científico, pero que hace tiempo asumió que debía elegir entre eso o no ser un buen padre (un padre presente y responsable en igualdad de condiciones que la madre de su hija). Eligió esto segundo y sí, puede que le pase factura a nivel «profesional» pues su nombre nunca acabará (aunque puede que sí lo haga) en las páginas de un libro de Peter Watson… y sin embargo, él no lo cambia. Y yo a él tampoco.

Es alguien de quien estoy altamente orgulloso… y en gran parte es por esta coherencia vital con la que vive. Ejemplar. Desde luego, yo lo tengo clarísimo: le prefiero a esos presuntos genios… presuntuosos. Y me siento tremendamente afortunado de que me considere su amigo.

Los átomos son huecos

Quizá mi influencia por las matemáticas me ha llevado a pensar que lo más importante del descubrimiento de los elementos atómicos, de los tipos de átomos que existen, lo básico de la naturaleza de la materia, es el hecho de que se parecen al teorema fundamental de la aritmética aplicada al mundo físico:

Fascinado por el platonismo y cierta pasión por la teoría pura, cierto pitagorismo de siglo XXI, hay algo que me fascinaba en el hecho de que la totalidad del universo estuviese conformada por una serie de partículas elementales (no importa si ahora esas partículas se ha demostrado que son a su vez combinaciones de otras partículas subatómicas). Ladrillos elementales a partir de los cuales se construye el todo, como esos números primos que componen cualquier otro número racional, mediante la división de todo número entero entre otro número entero descomponibles ambos en sus correspondientes únicos productos de números primos.

No había atendido a la estructura atómica, aunque relacionada con la misma de forma unívoca, es decir, la estructura atómica define el elemento al que pertenece el mismo átomo. A lo que no había atendido era a la disposición de esas partes subatómicas en el átomo. Miraba la parte meramente material y no lo inmaterial:

Hoy, leyendo el libro de IDEAS del siglo XX, de Peter Watson, he vuelto a atender a los experimentos de Rutherford y lo más llamativo ha resultado ser el hecho de que en realidad los átomos son prácticamente vacíos. Es decir están conformados por cargas centrales y cargas deslocalizadas alrededor suyo pero esencialmente espacio vacío. ¡Espacio vacío! La materia es atravesable, sí: atravesable por otra materia, con lo que solemos entender como frontera por tanto carece absolutamente de sentido pues todo es interpenetrable por todo.

¿No resulta sorprendente o paradójico visualizar un universo de vacío y sin embargo sentir que todo está lleno de algo?

Poesía cuántica

Querría escribir poesía cuántica
pero no tengo el nivel
(energético)
suficiente.

Nivel para estar en órbita
deslocalizado
incierto
y sin embargo…

Querría escribir poesía cuántica
y salirme por la tangente
por efecto poetoeléctrico
con una cinética que me arrancase
de la depresión
(energética)
en la que encuentro equilibrio.

uno imagina irracionales…

Uno imagina cuando encuentra por primera vez números a los que llama irracionales que no lo son en el sentido que ha imaginado, sino en el hecho de que no son razones, razones entre números enteros, pero tampoco uno cae en la cuenta de que a las divisiones les llamamos razones, así, sin ton ni son o todo lo contrario, quizá no hay nada más razonable que dividir las cosas, repartirlas, incluso los números enteros para que dejen de ser tan pretenciosamente enteros y cuando uno se encuentra números que no son el fruto de una repartición siente cierta aversión hacia ellos, los repudia, los niega, los ningunea, uno intenta convencerse de que son aproximaciones de algo más «razonable», aunque uno llegue a saber que no es así por reducción al absurdo, que parece una reducción al Pedro Ximénez, pero no tiene nada que ver con ella, por muy sabrosa que pueda resultar en ocasiones.

Uno imagina cuando encuentra por primera vez números a los que llama irracionales que no son todos iguales y que el loco paralelismo prestado por el léxico filosófico sirve para clasificarlos en trascendentes, construibles, algebraicos, normales… Sí, también uno descubre que hay números normales y lo que a uno le vuelve aún más loco (que no irracional) es que todo número normal debe ser necesariamente irracional, así, como si nada, como si eso de repente explicase tantas cosas que uno nunca ha comprendido en la vida que parece una epifanía.

Uno imagina cuando encuentra por primera vez números a los que llama irracionales que no son el final de todos los números posibles y que ha de haber algo más allá, así que se emociona incluso cuando a uno le hablan de los números imaginarios que hacen realidad el hecho de que los números reales no sean tan completos como creían ser, mientras sí lo serán los números complejos, así: completos sin complejos.

Uno imagina (pues no puede parar de imaginar) cuando encuentra por primera vez números a los que llama irracionales que no son más que la puerta de entrada a la matemática de la poesía, la que descubrirá un número poético que incluirá sus números imaginarios, sus irracionales, sus enteros y sus fracciones, sus negatividades, sus nulidades, la nada, nada infinita, nada lemniscática, nada redonda y pueril, nada feliz en la que uno se pierde sin dilación en una ecuación diferencial diferente a lo esperable, una nada inestimable, incalculable, una nada que forma operaciones como versos sueltos en un cosmos ingrávido.

Uno imagina cuando encuentra por primera vez números a los que llama irracionales que el amor debe de estar escondido en el número π o que la i no es la e, pero ambas comparten la letra como signo último al que referirse, en el que habitar, en el que albergarse hasta que paren de llover decimales si es que alguna vez escampa; uno va más allá del signo reconocible objetivamente para abrazar el grafo, el signo asémico, la línea más o menos continua que un material traza sobre otro rompiendo y rompiéndose a nivel atómico, destrozándose para dar vida a la imagen: imagen que imagina uno cuando encuentra por primera vez números a los que llama irracionales que no lo son en el sentido que ha imaginado.

Vacunaciones de la élite

Las infantas (siempre pienso en Las Meninas velazqueñas) se han vacunado saltándose, como no podía ser de otra manera, el protocolo que aplica a los demás ciudadanos del país.

Pero lejos de suponer un problema, lo veo como un servicio público, pues tanto esta irregularidad como otras de los miembros de la élite (porque hay una élite, casi inalcanzable), están sirviendo para que nos demos cuenta de lo deseables que son las vacunas, disipando de una manera rastrera el debate antivacuna o negacionista, sin más que añadir que ponerse por delante para mostrar su egoísmo.

Y como de egoísmos va el tema: todo el mundo quiere, ahora, vacunarse también. Bueno, pues bienvenida sea la idea, pues ha de alcanzarse un mínimo del 70% de personas vacunadas para que una enfermedad sea erradicada y pueda haber gente que diga que no necesita vacunarse para estar a salvo… dentro de ese 30% o menos de otra élite diferente, o no tanto.

Y seguimos…

Porcentajes

Encontrado este texto incrustado en una imagen en una red social, lo leo y resuelvo que es bastante acertado, aunque colocarlo en facebook no sea quizá la manera menos perversa de combatir lo que se denuncia.

No obstante, como todo en estas redes de incomunicación, ha desatado un pequeño debate que, ni mucho menos, estoy dispuesto a continuar. Tan sólo unos apuntes:

XXXXXXXX Dice:
Que estupidez más grande… EEUU cuenta con 769.000km2 de bosques naturales un 0,008% de toda su extensión y Rusia cuenta con 1.178.000km2 de bosques un 0,007% de su extensión.

YYYYYYYY Responde:
Creo que no has entendido lo que quiere decir. No habla de los bosques, sino más bien de la relación del capitalismo con la Ecología: nula relación, pues el capitalismo lo que busca es el beneficio económico, ningún otro.

Quería sumarme a lo dicho por YYYYYYYY, pero veo el ridículo de entablar batallas como esta en esos medios, así que me precipito a centrarme en otras cosas:

Si EEUU cuenta con 769.000 km2 bosques naturales de un total territorial de 9.147.593 km2, se trata de una fracción del 0,08406583, lo que aproximadamente equivale a un 8%, que es mil veces superior a los 0,008% que XXXXXXXX había dicho.

Si Rusia cuenta con 1.178.000 km2 bosques naturales de un total territorial de 17.125.191 km2, se trata de una fracción del 0,068787554, lo que aproximadamente equivale a un 7%, que es mil veces superior a los 0,007% que XXXXXXXX había dicho.

Es decir, que XXXXXXXX ha cometido dos errores de tres órdenes de magnitud en la medida: algo así como afirmar que yo mido más de mil quinientos metros de altura o «peso» más de 70 toneladas. Con alguien que comete estos errores, la compresión sobre lo que ese texto simplón incrustado en una imagen quieren decir, no es algo que se pueda dar por supuesta.

Pero ¿qué importa?

Nadie da importancia a las matemáticas. Al fin y al cabo, se trata de emitir opiniones basadas en vísceras, no en razonamientos. Cada día me parece más evidente. Y quizá no sea un problema. Siempre que nos reunamos con aquellas personas cuyas vísceras emitan los mismos gruñidos.

Esto no es una broma