Cuando las matemáticas pueden ser de vital importancia (vital es una palabra muy fuerte, pero a veces hay a quien le va la vida en ello).
Las matemáticas te sirven, también (especial hincapié en este «también», pues NO SOLO para las cosas prácticas ni para el dinero… sino para desarrollar tu mente, que no deja de ser algo práctico) para la vida diaria.
El otro día eché una mano a una persona que necesita traer algo de dinero desde un país sudamericano a España y se encuentra con el problema de que el envío le retiene un 10% del total del envío.
Por contra, los «bonachones» bancos le ofrecen un muy inferior interés del 3% anual sobre la cantidad que necesita y así no tiene necesidad de ese «usurero» 10%.
La realidad es que las matemáticas te ayudan a tomar la decisión en este mar plagado de tiburones: A partir del tercer año de 3%, en realidad se ha pagado un 10%. Así que si la cantidad es muy grande y no va a poder «amortizarse» o pagarse anticipadamente, lo mejor sería elegir ese 10%.
El crecimiento exponencial es lo que tiene.
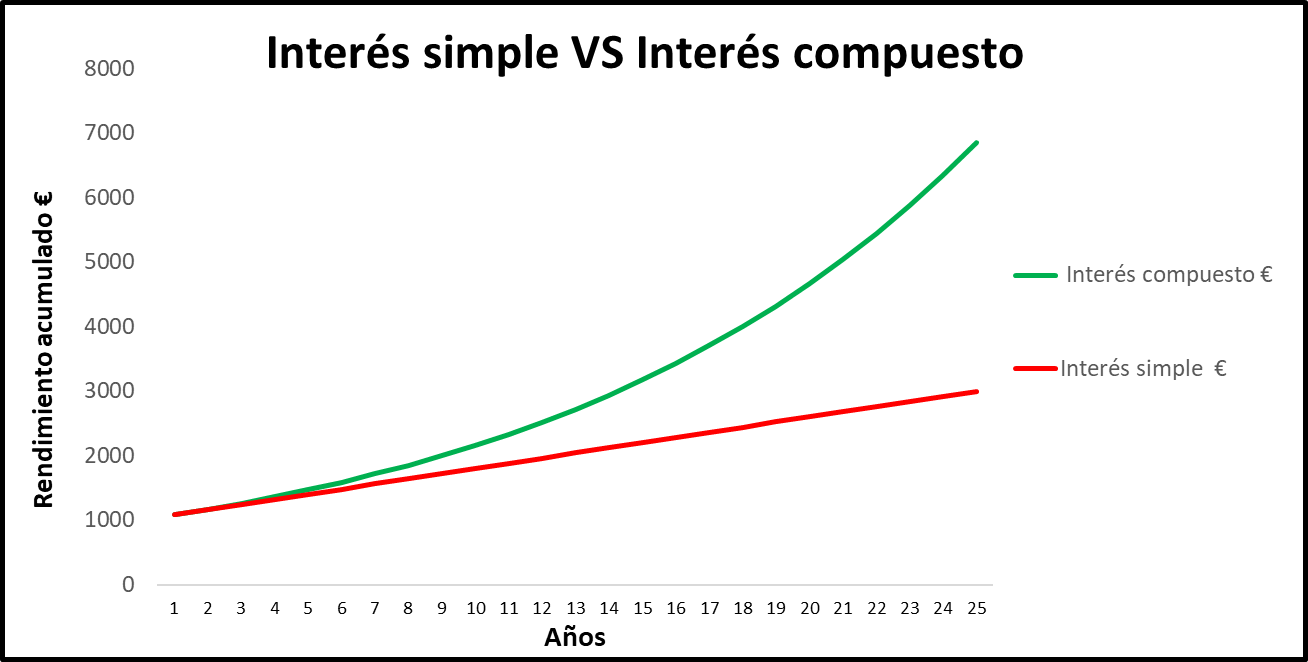
La fórmula que podría haberle enseñado alguien con anterioridad es bastante simple:
Cantidad Final (a pagar) = Cantidad Inicial x [(1 + interés) ^ años]
4% a 3 años = 1,043 = 1,126, lo que supone un 12,6% sobre la cantidad inicial. Así que cuidadito con que ese 3% suba una pequeña cantidad (de 3% a 4%) porque eso sube muy, muy rápido.
4% a 5 años ya es más del 20% de intereses y puede llegar (pronto) a ser el 100% de interés, es decir, tanto como la cantidad inicial.
Al 3%, la siguiente fórmula log(2)÷log(1,03) nos da como resultado que en 23 años se habría pagado más al banco que a la propiedad. Al 4%, tan solo en 17 años y al 5% en 14.
Así que igual la opción (usurera, no obstante) del 10% no está tan mal.