- Tractatus Logico-Philosophicus
 Introducción
IntroducciónEl Tractatus logico-philosophicus del profesor Wittgenstein intenta, consígalo o no, llegar a la verdad última en las materias de que trata, y merece por su intento, objeto y profundidad que se le considere un acontecimiento de suma importancia en el mundo filosófico. Partiendo de los principios del simbolismo y de las relaciones necesarias entre las palabras y las cosas en cualquier lenguaje, aplica el resultado de esta investigación a las varias ramas de la filosofía tradicional, mostrando en cada caso cómo la filosofía tradicional y las soluciones tradicionales proceden de la ignorancia de los principios del simbolismo y del mal empleo del lenguaje.
Trata en primer lugar de la estructura lógica de las proposiciones y de la naturaleza de la inferencia lógica. De aquí pasamos sucesivamente a la teoría del conocimiento, a los principios de la física, a la ética y, finalmente, a la mística (das Mystiche).
Para comprender el libro de Wittgenstein es preciso comprender el problema con que se enfrenta. En la parte de su teoría que se refiere al simbolismo se ocupa de las condiciones que se requieren para conseguir un lenguaje lógicamente perfecto. Hay varios problemas con relación al lenguaje. En primer lugar está el problema de qué es lo que efectivamente ocurre en nuestra mente cuando empleamos el lenguaje con la intención de significar algo con él; este problema pertenece a la psicología. En segundo lugar está el problema de la relación existente entre pensamientos, palabras y proposiciones y aquello a lo que se refieren o significan; este problema pertenece a la epistemología. En tercer lugar está el problema de usar las proposiciones-de tal modo que expresen la verdad antes que la falsedad; esto pertenece a las ciencias especiales que tratan de las materias propias de las proposiciones -en cuestión. En cuarto lugar está la cuestión siguiente: ¿Qué relación debe haber entre un hecho (una proposición, por ejemplo) y otro hecho para que el primero sea capaz de ser un símbolo del segundo?
Esta última es una cuestión lógica y es precisamente la única de que Wittgenstein se ocupa. Estudia las condiciones de un simbolismo correcto, es decir, un simbolismo en el cual una proposición «signifique» algo suficientemente definido. En la práctica, el lenguaje es siempre más o menos vago, ya que lo que afirmamos no es nunca totalmente preciso. Así pues, la lógica ha de tratar de dos problemas en relación con el simbolismo: l.° Las condiciones para que se dé el sentido mejor que el sinsentido en las combinaciones de símbolos; 2.º Las condiciones para que exista unicidad de significado o referencia en los símbolos o en las combinaciones de símbolos. Un lenguaje lógicamente perfecto tiene reglas de sintaxis que evitan los sinsentidos, y tiene símbolos articulares con un significado determinado y único. Wittgenstein estudia las condiciones necesarias para un lenguaje lógicamente perfecto. No es que haya lenguaje lógicamente perfecto, o que nosotros nos creamos aquí y ahora capaces e construir un lenguaje lógicamente perfecto, sino que toda función del lenguaje consiste en tener significado y sólo cumple esta función satisfactoriamente en la medida en que se aproxima al lenguaje ideal que nosotros postulamos.
La función esencial del lenguaje es afirmar o negar los hechos. Dada la sintaxis de un lenguaje, el significado de una proposición está determinado tan pronto como se conozca el significado de las palabras que la componen. Para que una cierta proposición pueda afirmar un cierto he debe haber, cualquiera que sea el modo como el lenguaje esté construido, algo en común entre la estructura de la proposición y la estructura del hecho. Esta es tal vez la tesis más fundamental de la teoría de Wittgenstein. Aquello que-haya de común entre la proposición y el hecho, no puede, así lo afirma el autor, decirse a su vez en el lenguaje. Sólo puede ser, en la fraseología de Wittgenstein, mostrado, no dicho, pues cualquier cosa que podamos decir tendrá siempre la misma estructura.
El primer requisito de un lenguaje ideal sería tener un solo nombre para cada elemento, y nunca el mismo nombre para dos elementos distintos. Un nombre es un símbolo simple en el sentido de que no posee partes que sean a su vez símbolos. En un lenguaje lógicamente perfecto, nada que no fuera un elemento tendría un símbolo simple. El símbolo para un compuesto sería un «complejo». Al hablar de un «complejo» estamos, como veremos más adelante, pecando en contra de las reglas de la gramática filosófica, pero esto es inevitable al principio. «La mayor parte de las proposiciones y cuestiones que se han escrito sobre materia filosófica no son falsas, sino sinsentido. No podemos, pues, responder a cuestiones de esta clase de ningún modo, sino establecer su sinsentido. La mayor parte de las cuestiones y proposiciones de los filósofos proceden de que no comprendemos la lógica de nuestro lenguaje. Son del mismo tipo que la cuestión de si lo bueno es más o menos idéntico que lo bello» (4.003). Lo que en el mundo es complejo es un hecho. Los hechos que no se componen de otros hechos son lo que Wittgenstein llama Sachverhalte, mientras que a un hecho que conste de dos o más hechos se le llama Tatsache; así, por ejemplo: «Socrates es sabio» es un Sachverhalt y también un Tatsache, mientras que «Sócrates es sabio y Platón es su discípulo» es un Tatsache, pero no un Sachverhalt.
Wittgenstein compara la expresión lingüística a la proyección en geometría. Una figura geométrica puede, ser pro yectada de varias maneras: cada una de éstas corresponde a un lenguaje diferente, pero las propiedades de proyección de la figura original permanecen inmutables, cualquiera que sea el modo de proyección que se adopte. Estas propiedades proyectivas corresponden a aquello que en la teoría de Wittgenstein tienen en común la proposición y el hecho, siempre que la proposición asevere el hecho.
En cierto nivel elemental esto desde luego es obvio. Es imposible, por ejemplo, establecer una afirmación, sobre dos hombres (admitiendo por ahora que los hombres puedan ser tratados como elementos) sin emplear dos nombres, y si se quiere aseverar una relación entre los dos hombres será necesario que la proposición en la que hacemos la aseveración establezca una relación entre los dos nombres. Si decimos «Platón ama a Sócrates», la palabra «ama», que está entre o la palabra «Platón» y la palabra «Sócrates», establece una relación entre estas dos palabras, y se debe a este hecho que nuestra proposición sea capaz de aseverar una relación entre las personas representadas por las palabras «Platón y Sócrates». «No: `El signo complejo aRb dice que a está en la relación R con b’, sino: Que a está en una cierta relación con b, dice que aRb» (3.1432).
Wittgenstein empieza su teoría del simbolismo con la siguiente afirmación (2.1):
«Nosotros nos hacemos figuras de los hechos.» Una figura, dice, es un modelo de la realidad, y a los objetos en la realidad corresponden los elementos de la figura: la figura misma es un hecho.
El hecho de que las cosas tengan una cierta relación entre sí se representa por el hecho de que en la figura sus elementos tienen también una cierta relación, unos con otros. En la figura y en lo figurado debe haber algo idéntico para que una pueda ser figura de lo otro completamente. Lo que la figura debe tener en común con la realidad para poder figurarla a su modo y manera -justa o falsamente- es su forma de figuración» (2.161, 2.17).
Hablamos de una figura lógica de la realidad; cuando queremos indicar solamente tanta semejanza cuanta es esencial a su condición de ser una figura, y esto en algún sentido, es decir, cuando no deseamos implicar nada más que la identidad de la forma lógica. La figura lógica de un hecho, dice, es un Gedanke. Una figura puede corresponder o no corresponder al hecho y por consiguiente ser verdadera o falsa, pero en ambos casos tiene en común con el hecho la forma lógica. El sentido en el cual Wittgenstein habla de figuras puede ilustrarse por la siguiente afirmación: «El disco gramofónico, el pensamiento musical, la notación musical; las ondas sonoras, están todos, unos respecto de otros, en aquella internó relación figurativa que se mantiene entre lenguaje y mundo. A todo esto es común la estructura lógica. (Como en la fábula, los dos jóvenes, sus dos caballos y sus lirios, son todos, en cierto sentido, la misma cosa)» (4.014). La posibilidad de que una proposición represente a un hecho depende del hecho de que en ella los objetos estén representados por signos. Las llamadas «constantes» lógicas no están representadas por signos, sino que ellas mismas están presentes tanto en la proposición como en el hecho. La proposición y el hecho deben manifestar la misma «multiplicidad» lógica, que no puede ser a su vez representada, pues tiene que tener en común el hecho y la figura. Wittgenstein sostiene que todo aquello que es propiamente filosófico pertenece a lo que sólo se puede expresar, es decir: a aquello que es común al hecho y a su figura lógica. Según este criterio se concluye que nada exacto puede decirse en filosofía. Toda proposición filosófica es un error gramatical, y a lo más que podemos aspirar con la discusión filosófica es a mostrar a los demás que la discusión filosófica es un error. «La filosofía no es una de las ciencias naturales. (La palabra `filosofía’ debe significar algo que esté sobre o bajo, pero no junto a las ciencias naturales) E1 objeto de la filosofía es la aclaración lógica de pensamientos. La filosofía no es una teoría, sino una actividad. Una obra filosófica consiste especialmente en elucidaciones. El resultado de la filosofía no son `proposiciones filosóficas’ sino el esclarecimiento de las proposiciones. La filosofía debe esclarecer y delimitar con precisión los pensamientos que de otro modo serían, por así decirlo, opacos y confusos» (4.111 y 4.112). De acuerdo con este principio todas las cosas que diremos para que el lector comprenda la teoría de Wittgenstein son todas ellas cosas que la propia teoría condena como carentes de sentido. Teniendo en cuenta esto, intentaremos exponer la visión del mundo que parece que está al fondo de su sistema.
El mundo se compone de hechos: hechos que estrictamente ha blando no podemos definir, pero podemos explicar lo que queremos decir admitiendo que los hechos son los que hacen á las proposiciones verdaderas o falsas. Los hechos pueden contener partes que sean hechos o pueden no contenerlas; «Sócrates era un sabio ateniense» se compone de dos hechos:
«Sócrates era sabio» y «Sócrates era un ateniense». Un hecho que no tenga partes que sean hechos se llama por Wittgenstein Sachverhalt. Es lo mismo que aquello a lo que llama hecho atómico. Un hecho atómico, aunque no conste de partes que son hechos, sin embargo consta de partes. Si consideramos «Sócrates es sabio» como un hecho atómico veremos que contiene los constitutivos «Sócrates» y «sabio». Si se analiza un hecho atómico lo más completamente posible (posibilidad teórica, no práctica), las partes constitutivas que se obtengan al final pueden llamarse «simples» u «objetos». Wittgenstein no pretende que podamos realmente aislar el «simple» o que tengamos de él un conocimiento empírico. Es una necesidad lógica exigida por la teoría como el caso del electrón. Su fundamento para sostener que hay simples es que cada complejo presupone un hecho. Esto no supone necesariamente que la complejidad de los hechos sea finita; aunque cada hecho constase de infinidad de hechos atómicos y cada hecho atómico se compusiese de un número infinito de objetos, aun en este supuesto debería haber objetos y hechos atómicos (4.2211). La afirmación de que hay un cierto complejo se reduce a la aseveración de que sus elementos constitutivos están en una cierta relación, que es la aseveración de un hecho; así, pues, si damos un nombre al complejo, este nombre sólo tiene sentido en virtud de la verdad de una cierta proposición, especialmente la proposición que arma que los componentes del complejo están en esa relación. Así, nombrar a los complejos presupone la proposición, mientras que las proposiciones presuponen que los simples tengan un nombre. Así, pues, se pone de manifiesto que nombrar los simples es lógicamente lo primero en lógica.
El mundo está totalmente descrito si todos los hechos atómicos se conocen, unido al hecho de que éstos son todos los hechos. El mundo no se describe por el mero nombrar de todos los objetos que están en él; es necesario también conocer los hechos atómicos de los cuales esos objetos son partes constitutivas. Dada la totalidad de hechos atómicos, cada proposición verdadera, aunque compleja, puede teóricamente ser inferida. A una proposición (verdadera o falsa) que asevera un hecho atómico se le llama una proposición atómica. Todas las proposiciones atómicas son lógicamente independientes unas de otras. Ninguna proposición atómica implica otra o es compatible con otra. Así pues, todo el problema de la inferencia lógica se refiere a proposiciones que no son atómicas. Tales proposiciones pueden ser llamadas moleculares.
La teoría de Wittgenstein de las proposiciones moleculares se fundamenta sobre su teoría acerca de la construcción de las funciones de verdad.
Una función de verdad de una proposición p es una proposición que contiene a p, de modo que su verdad o falsedad depende sólo de la verdad o falsedad de p;. del mismo modo, una función de verdad de varias proposiciones p, q, r... es una proposición que contiene p, q, r..., y así su verdad o falsedad depende sólo de la verdad o de la falsedad de p, q, r... Pudiera parecer a primera vista que hay otras funciones de proposiciones además de las funciones de verdad; así, por ejemplo, sería «A cree p», ya que de modo general A creería algunas proposiciones verdaderas y algunas falsas; a menos que sea un individuo excepcionalmente dotado, no podemos colegir que p es verdadera por el hecho de que lo crea, o que p es falsa por el hecho de que no lo crea. Otras excepciones aparentes serian, -por ejemplo, «p es una proposición muy compleja» o «p es una proposición referente a Sócrates». Wittgenstein sostiene, sin embargo, por razones que -ya expondremos, que tales excepciones son sólo apa - rentes, y que cada función de una proposición es realmente una función de verdad. De aquí se sigue que si podemos definir las funciones de verdad de modo general, podremos obtener una definición general de todas las proposiciones en los términos del grupo -primitivo de las proposiciones atómicas. De este modo procede Wittgenstein.
Ha sido demostrado por el doctor Sheffer (Trans. Am. Math. Soc., vol. XIV, pp. 481-488) que todas las funciones de verdad de un grupo dado de proposiciones pueden construirse a partir de una de estas dos funciones: «no-p o no-q» o «no-p y no-q». Wittgenstein emplea la última, presuponiendo, el conocimiento del trabajo del doctor Sheffer. Es fácil ver el modo en que se construyen otras funciones de verdad de «no-p y no-q». «No-p y no-p» es equivalente a
«no-p», con lo que obtenemos una definición de la negación en los términos de nuestra función primitiva; por lo tanto, podemos definir «p o q», puesto que es la negación de «no-p» y «no-q»; es decir, de nuestra función primitiva; por lo tanto, podemos definir «p o q», puesto que es la negación de «no-p» y «no-q»; es decir de nuestra función primitiva. El desarrollo de otras funciones de verdad de «no-p» y «p o q» se dan detalladamente al comienzo de Principia Mathematica. Con esto se logra lo que pretendemos, cuando las proposiciones que son los argumentos de nuestras funciones de verdad se dan por enumeración. Wittgenstein, sin embargo, por un análisis realmente interesante, consigue extender el proceso a las proposiciones generales, es decir, a los casos en que las proposiciones que son argumentos de nuestras funciones de verdad no están dadas por enumeración, sino que se dan como todas las que cumplen cierta condición. Por ejemplo, sea fx una función proposicional (es decir, una función cuyos valores son proposiciones), lo mismo que «x es humano» -entonces los diferentes valores fx constituyen un grupo de proposiciones. Podemos extender la idea «no-p y no-q» tanto como aplicarla a la negación simultánea de todas las proposiciones que son valores de fx. De este modo llegamos a la proposición que de ordinario representa en lógica matemática por las palabras «fx es falsa para todos los valores de x». La negación de esto sería la proposición «hay al menos una x para la cual fx es verdad» que está representada por «(Ýx).fx». Si en vez de fx hubiésemos partido de no-fx habríamos llegado a la proposición «fx es verdadera para todos los valores de x», que está representada por «(x).fx». El método de Wittgenstein para operar con las proposiciones generales [es decir «(x).fx» y «(Ýx).fx »] difiere de los métodos precedentes por el hecho de que la generalidad interviene s en la especificación del grupo de proposiciones a que se refiere, y cuando esto se lleva a cabo, la construcción de las funciones de verdad procede exactamente, como en el caso de un número finito de argumentos dados, por enumeración, p, q, r...
Sobre este punto, Wittgenstein no da en el texto una explicación suficiente de su simbolismo. El símbolo que emplea es (-p, -î, N(-î)). He aquí la explicación de este simbolismo:
-p representa todas las proposiciones atómicas.
-î representa cualquier grupo de proposiciones.
N (-î) representa la negación de todas las proposiciones que componen -î.
El símbolo completo (-p, -î, N(-î)) significa todo aquello que puede obtenerse seleccionando proposiciones atómicas, negándolas todas, seleccionando algunas del grupo de proposiciones nuevamente obtenido unidas con otras del grupo primitivo -y así indefinidamente-.Esta es, dice, la función general de verdad y también la forma general de la proposición. Lo que esto significa es algo menos complicado de lo que parece. El símbolo intenta describir un proceso con la ayuda del cual, dadas las proposiciones atómicas, todas las demás pueden construirse. El proceso depende de:
(a) La prueba-de Sheffer de que todas- las funciones de verdad pueden obtenerse de la negación simultánea, es decir, de «no-p y no-q»;
(b) La teoría de Wittgenstein de la derivación de las proposiciones generales de las conjunciones y disyunciones;
(c) La aseveración de que una proposición puede encontrarse en otra sólo como argumento de una función de verdad.
Dados estos tres fundamentos, se sigue que todas las proposiciones que no son atómicas pueden derivarse de las que lo son por un proceso uniforme, y es este proceso el que Wittgenstein indica en su símbolo.
Por este método uniforme de construcción llegamos a una asombrosa simplificación de la teoría de la inferencia, lo mismo que a una definición del tipo de proposiciones que pertenecen a la lógica. El método de operación descrito autoriza a Wittgenstein a decir que todas las proposiciones pueden construirse del modo anteriormente indicado, partiendo de las proposiciones atómicas, y de este modo queda definida la totalidad de las proposiciones. (Las aparentes excepciones mencionadas más arriba son tratadas de un modo que consideraremos más adelante.) Wittgenstein puede, pues, afirmar que proposiciones son todo lo que se sigue de la totalidad de las proposiciones atómicas (unido al hecho de que ésta es la totalidad de ellas); que una proposición es siempre una función de verdad de las proposiciones atómicas; y de que si p se sigue de q, el significado de p está contenido en el significado de q; de lo cual resulta, naturalmente, que nada puede deducirse de una proposición atómica Todas las proposiciones de la lógica, afirma, son tautologías, como, por ejemplo, «p o no p».
El hecho de que nada puede deducirse de una proposición atómica tiene aplicaciones de interés, por ejemplo, a la causalidad. En la lógica de Wittgenstein no puede haber nada semejante al nexo causal. «Que el sol vaya a surgir mañana es una hipótesis. No sabemos, realmente, si surgirá, ya que no hay necesidad alguna para que una cosa acaezca porque acaezca otra.»
Tomemos ahora otro tema -el de los nombres. En el lenguaje lógico-teorético de Wittgenstein, los nombres sólo son dados a los simples. No damos dos nombres a una sola cosa, o un nombre a dos cosas. No hay ningún medio, según el autor, para describir la totalidad de las cosas que pueden ser nombradas; en otras palabras, la totalidad de todo cuanto hay en el mundo. Para poder hacer esto tendríamos que conocer alguna propiedad que perteneciese a cada cosa por necesidad lógica. Se ha intentado alguna vez encontrar tal propiedad en la auto-identidad; pero la concepción de la identidad está sometida por Wittgenstein a un criticismo destructor, del cual no parece posible escapar. Queda rechazada la definición de la identidad por medio de la identidad de lo indiscernible, porque la identidad de lo indiscernible parece que no es un principio lógico necesario. De acuerdo con este principio, x es idéntica a y si cada propiedad de x es una propiedad de y; pero, después de todo, seria lógicamente posible para ambas cosas que tuviesen exactamente las mismas propiedades. Que esto de hecho no ocurra, es una característica accidental del mundo, no una característica lógicamente necesaria, y las características accidentales del mundo no deben naturalmente ser admitidas en la estructura de la lógica. Wittgenstein, de acuerdo con esto, suprime la identidad y adopta la convención de que diferentes letras signifiquen diferentes cosas. En la práctica se necesita la identidad, por ejemplo, entre un nombre y una descripción o entre dos descripciones. Se necesita para proposiciones tales como «Sócrates es el filósofo que bebió la cicuta» o «El primer número par es aquel que sigue inmediatamente a 1.» Es fácil en el sistema de Wittgenstein proveer respecto de tales usos de la identidad.
La exclusión de la identidad excluye un método de hablar de la totalidad de las cosas, y se encontrará que cualquier otro método que se proponga ha de resultar igualmente engañoso; así, al menos, lo afirma Wittgenstein, y yo creo que con fundamento. Esto equivale a decir que
«objeto» es un seudoconcepto. Decir que «x es un objeto» es no decir nada. Sigue esto de que no podemos hacer juicios tales como «hay más de tres objetos en el mundo» o «hay un número infinito de objetos en el mundo». Los objetos sólo pueden mencionarse en conexión con alguna propiedad definida. Podemos decir «hay más de tres objetos que son humanos», o «hay más de tres objetos que son rojos», porque en estas afirmaciones la palabra «objeto» puede sustituirse en el lenguaje de la lógica por una variable que será en el primer caso la función «x es humano»; en el segundo, la función «x es rojo». Pero cuando intentamos decir «hay más de tres objetos», esta sustitución de la variable por la palabra «objeto» se hace imposible, y la proposición, por consiguiente, carece de sentido.
Henos, pues, aquí ante un ejemplo de una tesis fundamental de Wittgenstein, que es imposible decir nada sobre el mundo como un todo, y que cualquier cosa que pueda decirse ha de ser sobre partes del mundo. Este punto de vista puede haber sido en principio sugerido por la notación, y si es así, esto dice mucho en su favor, pues una buena notación posee una penetración y una capacidad de sugerir que la hace en ocasiones parecerse a una enseñanza viva. Las irregularidades en la notación son con frecuencia el primer signo de los errores filosóficos, y una notación perfecta llegaría a ser un sustitutivo del pensamiento. Pero aun cuando haya sido la notación la que haya sugerido al principio a Wittgenstein la limitación de la lógica a las cosas del mundo, en contraposición al mundo como a un todo, no obstante, esta concepción, una vez sugerida, ha mostrado encerrar mucho más que la simple notación. Por mi parte, no pretendo saber si esta tesis es definitivamente cierta. En esta introducción, mi objeto es exponerla, no pronunciarme respecto de ella. De acuerdo con este criterio, sólo podríamos decir cosas sobre el mundo como un todo si pudiésemos salir fuera del mundo, es decir, si dejase para nosotros de ser el mundo. Pudiera ocurrir que nuestro mundo estuviese limitado por algún ser superior que lo vigilase sobre lo alto; pero para nosotros, por muy finito que pueda ser, no puede tener límites el mundo desde el momento en que no hay nada fuera de él. Wittgenstein emplea como una imagen la del campo visual. Nuestro campo visual no tiene para nosotros límites visuales, ya que no existen fuera de él, del mismo modo que en nuestro mundo lógico no hay límites lógicos, ya que nuestra lógica no conoce nada fuera de ella.
Estas consideraciones le llevan a una discusión interesante sobre el solipsismo. La lógica, dice, llena el mundo. Los límites del mundo son también sus propios límites. En lógica, por consiguiente, no podemos decir: en el mundo hay esto y lo otro, pero no lo de más allá; decir esto presupondría efectivamente excluir ciertas posibilidades, y esto no puede ser, ya que requeriría que la lógica atravesase los límites del mundo, como sí contemplase estos límites desde el otro lado. Lo que no podemos pensar, no podemos pensar; por consiguiente, tampoco podemos decir lo que no podemos pensar.
Esto, dice Wittgenstein, da la clave respecto del solipsismo. Lo que el solipsismo pretende es ciertamente correcto; pero no puede decirse, sólo puede mostrarse. Que el mundo es mi mundo se muestra en el hecho de que los límites del lenguaje (el único lenguaje que yo entiendo) indican los límites de mi mundo. El sujeto metafísico no pertenece al mundo; es un límite del mundo.
Debemos tratar ahora la cuestión de las proposiciones moleculares que no son a pri mera vista funciones de verdad de las proposiciones que contienen; por ejemplo: «A cree p».
Wittgenstein introduce este argumento en defensa de su tesis; a saber: que todas las funciones moleculares son funciones de verdad. Dice (5.54): «En la forma proposicional general la proposición entra en otra sólo como base de las operaciones de verdad» A primera vista, continua diciendo, parece como si una proposición pudiera entrar de otra manera; por ejemplo: «A cree p». De manera superficial parece como si la proposición p estuviese en una especie de relación con el objeto A. «Pero es claro que “A cree p”, “A. piensa p”, “A dice p” son de la forma “‘p’ dice p”; y aquí de la coordinación de un hecho con un objeto, coordinación de hechos por medio de la coordinación de sus objetos» (5.542 ).
Lo que Wittgenstein expone aquí lo expone de modo tan breve que no queda bastante claro para aquellas personas que desconocen las controversias a las cuales se refiere.
La teoría con la cual se muestra en desacuerdo está expuesta en mis artículos sobre la naturaleza de la verdad y de la falsedad en Philosophical Essays y Proceedings of the Arisiotelian Society,
1906-1907. El problema de que se trata es el problema de la forma lógica de la fe, es decir, cuáles el esquema que representa lo que sucede cuando un hombre cree. Naturalmente, el problema se aplica no sólo a la fe, sino también a una multitud de fenómenos mentales que se pueden llamar actitudes proposicionales: duda, consideración, deseo, etc. En todos estos casos parece natural expresar el fenómeno en la forma «A duda p», «A desea p», etcétera, lo que hace que esto aparezca como si existiese una relación entre una persona y una proposición. Este, naturalmente, no puede ser el último análisis, ya que las personas son ficciones lo mismo que las proposiciones, excepto en el sentido en que son hechos. Una proposición, considerada como un hecho en sí mismo consistente, puede ser una serie de palabras que un hombre se repite a sí mismo, o una ima gen compleja, o una serie de imágenes que pasan por su imaginación, o una serie de movimientos corporales incipientes. Puede ser una cualquiera de estas innumerables diferentes cosas. La proposición, en cuanto un hecho en sí mismo consistente, por ejemplo, la serie actual de palabras que el hombre se dice a sí mismo, no tiene importancia para la lógica. Lo que es interesante para la lógica es el elemento común a todos estos hechos, los cuales permiten, como decimos, significar el hecho que la proposición asevera. Para la psicología, nat uralmente, es más interesante, pues un símbolo no significa aquello que simboliza sólo en virtud de una relación lógica, sino también en virtud de una relación psicológica de intención, de asociación o de cualquier otro carácter. La parte psicológica del significado no concierne, sin embargo, al lógico. Lo que le concierne en este problema de la fe es el esquema lógico. Es claro que cuando una persona cree una proposición, la persona considerada como un sujeto metafísico, no debe ser tenida en cuenta en orden a explicar lo que está sucediendo. Lo que ha de explicarse es la relación existente entre la serie de palabras, que es la proposición considerada como un hecho por sí mismo existente, y el hecho «objetivo» que hace a la proposición verdadera o falsa. Todo esto se reduce en último término a la cuestión del significado de las proposiciones, y es tanto como decir que el significado de las proposiciones es la única parte no psicológica del problema implicada en el análisis de la fe. Este problema es tan sólo el de la relación entre dos hechos, a saber: la relación entre las series de palabras empleadas por el creyente y el hecho que hace que estas palabras sean verdaderas o falsas. La serie de palabras es un hecho, tanto como pueda serlo aquello que hace que sea verdadera o falsa. La relación entre estos dos hechos no es inanalizable, puesto que el significado de una proposición resulta del significado de las palabras que la constituyen. El significado de la serie de palabras que es una proposición, es una función del significado de las palabras aisladas. Según esto, la proposición como un todo no entra realmente en aquello que ya se ha explicado al explicar el significado de la proposición. Ayudaría tal vez a comprender el punto de vista que estoy tratando de exponer, decir que en los casos ya tratados la proposición está presente como un hecho y no como una proposición. Tal afirmación no debe tomarse demasiada literalmente. El punto esencial es que en el acto de creer, de desear, etc., es lógicamente fundamental la relación de una proposición considerada como hecho con el hecho que la hace verdadera o falsa, y que esta relación entre dos actos es reducible a la relación de sus componentes. Así, pues, la proposición- entra-aquí de un modo completamente -distinto al modo como entra en una función de verdad.
Hay algunos aspectos, según mi opinión, en los que la teoría de Wittgenstein necesita un mayor desarrollo técnico. Esto puede aplicarse, concretamente, a su teoría del número (6.02 ss.), la cual, tal y como está, sólo puede aplicarse a los números finitos. Ninguna lógica puede considerarse satisfactoria hasta que se haya demostrado que es capaz de poder ser aplicada a los números transfinitos. No creo que haya nada en el sistema de Wittgenstein que le impida llenar esta laguna.
Más interesante que estas cuestiones de detalle comparativo es la actitud de Wittgenstein respecto de la mística. Su actitud hacia ella nace de modo natural de su doctrina de lógica pura, según la cual, la proposición lógica es una figura (verdadera o falsa) del hecho, y tiene en común con el hecho una cierta estructura. Es esta estructura común lo que la hace capaz de ser una figura del hecho; pero la estructura no puede, a su vez, ponerse en palabras, puesto que es la estructura de las palabras, lo mismo que de los hechos a los cuales se refiere. Por consiguiente, todo cuanto quede envuelto en la idea de la expresividad del lenguaje, debe permanecer incapaz de ser expresado en el lenguaje, y es, por consiguiente, inexpresable en un sentido perfectamente preciso. Este inexpresable contiene, según Wittgenstein, el conjunto de la lógica y de la filosofía.
El verdadero método de enseñar filosofía, dice, sería limitarse a las proposiciones de las ciencias, establecidas con toda la claridad y exactitud posibles, dejando las afirmaciones filosóficas al discípulo, y haciéndole patente que cualquier cosa que se haga con ellas carece de significado. Es cierto que la misma suerte que le cupo a Sócrates podría caberle a cualquier hombre que intentase este método de enseñanza; pero no debemos atemorizarnos, pues éste es único método justo. No es precisamente esto lo que hace dar respecto de aceptar o no la posición de Wittgenstein, a pesar de los argumentos tan poderosos que ofrece como base. Lo que ocasiona tal duda es el hecho de que después de todo, Wittgenstein encuentra el modo de decir una buena cantidad de cosas sobre aquello de lo que nada se puede decir, sugiriendo así al lector escéptico la posible existencia de una salida, bien a través de la jerarquía de lengua bien de cualquier otro modo. Toda la ética, por ejemplo coloca Wittgenstein en la mística, región inexpresable. A pesar de ello, es capaz de comunicar sus opiniones éticas. Su defensa consistiría en decir que lo «místico» puede mostrarse, pero no decirse. Puede que esta defensa sea satisfactoria, pero por mi parte confieso que me produce una cierta sensación de disconformidad intelectual.
Hay un problema puramente lógico, con relación al cual esas dificultades son especialmente agudas. Me refiero al problema de la generalidad. En la teoría de la generalidad es necesario considerar todas las proposiciones de la forma fx, donde fx es una función proposicional dada. Esto pertenece a la parte de la lógica que puede expresarse de acuerdo con el sistema de Wittgenstein. Pero la totalidad de los posibles valores de x que puede parecer que están comprendidos en la totalidad de las proposiciones de la forma fx no está admitida por Wittgenstein entre aquellas cosas que pueden ser dichas, pues esto no es sino la totalidad de las cosas del mundo y esto supone el intento de concebir el mundo como un todo; «el sentido del mundo como un todo limitado es lo místico»; por lo tanto, la totalidad de los valores de x es la mística (6.45). Esto está expresamente dicho cuando Wittgenstein niega que podamos construir proposiciones sobre el número de cosas que hay en el mundo, como, por ejemplo, cuando decimos que hay más de tres.
Estas dificultades me sugieren la siguiente posibilidad: que todo lenguaje tiene, como Wittgenstein dice, una estructura de la cual nada puede decirse en el lenguaje, pero que puede haber otro lenguaje que trate de la estructura del primer lenguaje y que tenga una nueva estructura y que esta jerarquía de lenguaje no tenga límites. Wittgenstein puede responder que toda su teoría puede aplicarse sin cambiarla a la totalidad de estos lenguajes. La única réplica sería negar que exista tal totalidad. La totalidad de la que Wittgenstein sostiene que es imposible hablar lógicamente, está sin embargo pensada por él como existente y constituye el objeto de su mística. La totalidad resultante de nuestra jerarquía no sería, pues, inexpresable con un criterio meramente lógico, sino una ficción, una ilusión, y en este sentido la supuesta esfera de la mística quedaría abolida. Tal hipótesis es muy difícil y veo objeciones a las cuales, de momento, no sé cómo contesta, aunque no veo cómo una hipótesis más fácil pueda escaparse de las conclusiones de Wittgenstein. Aunque esta hipótesis es tan difícil que pudiese sostenerse, dejaría intacta una gran parte de la teoría de Wittgenstein; aunque posiblemente no aquella parte en al cual insiste más. Teniendo larga experiencia de las dificultades de la lógica y de lo ilusorio de las teorías que parecen irrefutables, no soy capaz de asegurar la exactitud de una teoría fundándome tan sólo en que no veo ningún punto en que esté equivocada. Pero haber construido una teoría lógica, que no es en ningún punto manifiestamente errónea, significa haber logrado una obra de extraordinaria dificultad e importancia. Este mérito, en mi opinión, corresponde al libro de Wittgenstein y lo convierte en algo que ningún filósofo serio puede permitirse descuidar.
Bertrand Russell, Mayo, 1922.
 Prólogo
PrólogoQuizás este libro sólo puedan comprenderlo aquellos que por si mismos hayan pensado los mismos o parecidos pensamientos a los que aquí se expresan. No es por consiguiente un manual. Habrá alcanzado su objeto si logra satisfacer a aquellos que lo leyeren entendiéndolo.
El libro trata de problemas de filosofía y muestra, al menos así lo creo, que la formulación de estos problemas descansa en la falta de comprensión de la lógica de nuestro lenguaje. Todo el significado del libro puede resumirse en cierto modo en lo siguiente: Todo aquello que puede ser dicho, puede decirse con claridad: y de lo que no se puede hablar, mejor es callarse.
Este libro quiere, pues, trazar unos límites al pensamiento, o mejor, no al pensamiento, sino a la expresión de los pensamientos; porque para trazar un límite al pensamiento tendríamos que ser capaces de pensar ambos lados de este límite, y tendríamos por consiguiente que ser capaces de pensar lo que no se puede pensar.
Este límite, por lo tanto, sólo puede ser trazado en el lenguaje y todo cuanto quede al otro lado del límite será simplemente un sinsentido.
De en qué medida coincidan mis esfuerzos con los de los demás filósofos no quiero juzgar. En efecto, lo que yo aquí he escrito no tiene ninguna pretensión de novedad en particular. Por consiguiente no menciono las fuentes, porque es para mí indiferente que aquello que yo he pensado haya sido pensado por alguien antes que yo.
Sólo quiero hacer constar que a la gran obra de Frege y a los escritos de mi amigo Bertrand Russell debo una gran parte de las motivaciones de mis pensamientos.
Si este libro tiene algún valor, este valor radica en dos cosas: Primero, que en él se expresan pensamientos, y este valor será mayor cuanto mejor estén expresados los pensamientos, cuanto más se haya remachado el clavo. Soy consciente, aquí, de no haber profundizado todo lo posible. Simplemente por esto, porque mis fuerzas son insuficientes para lograr esta tarea. Puedan otros emprenderla y hacerlo mejor.
Por otra parte la verdad de los pensamientos aquí comunicados me parece intocable y definitiva. Soy, pues, de la opinión de que los problemas han sido, en lo esencial, finalmente resueltos. Y si no estoy equivocado en esto, el valor de este trabajo consiste, en segundo lugar, en el hecho de que muestra cuán poco se ha hecho cuando se han resuelto estos problemas.
Viena, 1918. L. W.
 1. El mundo es todo lo que acaece.
1. El mundo es todo lo que acaece.- 1.1 El mundo es la totalidad de los hechos, no de las cosas.
- 1.11 El mundo está determinado por los hechos y por ser todos los hechos.
- 1.12 Porque la totalidad de los hechos determina lo que acaece y también lo que no acaece.
- 1.13 Los hechos en el espacio lógico son el mundo.
- 1.2 El mundo se divide en hechos.
- 1.21 Una cosa puede acaecer o no acaecer y el resto permanece igual.
 2 Lo que acaece, el hecho, es la existencia de los hechos atómicos.
2 Lo que acaece, el hecho, es la existencia de los hechos atómicos.- 2.0
- 2.01 El hecho atómico es una combinación de objetos (entidades, cosas).
- 2.011 Es esencial a la cosa poder ser la parte constitutiva de un hecho atómico.
- 2.012 En lógica, nada es accidental: si la cosa puede entrar en un hecho atómico, la posibilidad del hecho atómico debe estar ya prejuzgada en la cosa.
- 2.0121 Aparecería, por así decirlo, como un accidente si a una cosa capaz de existir por sí misma pudiese subsecuentemente convenirle un estado de cosas. Si las cosas pueden entrar en un hecho atómico, esta posibilidad debe estar ya en ellas. (Algo lógico no puede ser sólo-posible. La lógica trata de toda posibilidad y todas las posibilidades son sus hechos.) Lo mismo que no nos es posible pensar objetos espaciales fuera del espacio y objetos temporales fuera del tiempo, así no podemos pensar ningún objeto fuera de la posibilidad de su conexión con otros. Si yo puedo pensar el objeto en el contexto del hecho atómico, no puedo, sin embargo, pensarlo fuera de la posibilidad de ese contexto.
- 2.0122 La cosa es independiente en cuento puede entrar en todos los posibles estados de cosas, pero esta forma de independencia es una forma de dependencia. (Es imposible que las palabras se presenten de dos modos distintos, solas y en proposición.)
- 2.0123 Si yo conozco un objeto, conozco también todas sus posibilidades de entrar en los hechos atómicos. (Cada una de tales posibilidades debe estar contenida en la naturaleza del objeto.) No se puede encontrar posteriormente una nueva posibilidad.
- 2.01231 Para conocer un objeto no debo conocer sus propiedades externas, sino todas sus propiedades internas.
- 2.0124 Si todos los objetos son dados, también se dan con ellos todos los posibles hechos atómicos.
- 2.013 Cada cosa está, por así decirlo, en un espacio de posibles hechos atómicos. Puedo pensar esta área como vacía, pero no puedo pensar la cosa sin el área.
- 2.0131 Un objeto espacial debe encontrarse en un espacio infinito. (El punto en el espacio es un lugar de argumento.) Una mancha en el campo visual puede no ser rosa, pero debe tener un color; tiene, por así decirlo, un espacio color en torno suyo. El tono debe tener una altura, el objeto del tacto una dureza, etc.
- 2.014 Los objetos contienen la posibilidad de todos los estados de cosas.
- 2.0141 La posibilidad de entrar en hechos atómicos es la forma del objeto.
- 2.02 El objeto es simple.
- 2.020
- 2.0201 Todo aserto sobre complejos puede descomponerse en un aserto sobre sus partes constitutivas y en aquellas proposiciones que describen completamente el complejo.
- 2.021 Los objetos forman la sustancia del mundo. Por eso no pueden ser compuestos.
- 2.0211 Si el mundo no tuviese ninguna sustancia, dependería que una proposición tuviera sentido, de que otra proposición fuese verdadera.
- 2.0212 En este caso sería imposible trazar una figura (bild) del mundo (verdadera o falsa).
- 2.022 Es claro que por muy diferente del real que se imagine un mundo debe tener algo –una forma- en común con el mundo real.
- 2.023 Esta forma fija está constituida por los objetos.
- 2.0231 La sustancia del mundo puede determinar sólo una forma y ninguna propiedad material. Porque éstas se presentan primero en las proposiciones – están formadas primero por la configuración de los objetos.
- 2.0232 Dicho sea de paso: Los objetos son incoloros.
- 2.0233 Dos objetos de la misma forma lógica están –prescindiendo de sus propiedades externas- diferenciados el uno del otro sólo porque son diferentes.
- 2.02331 O una cosa tiene propiedades que ninguna otra tiene, y entonces se puede sin más, por una descripción, distinguirla de las otras y referirse a ella; o bien, hay más cosas que tienen en común la totalidad de sus propiedades, y entonces es absolutamente imposible señalar alguna de ellas. Porque si la cosa no se distingue por nada, yo no la puedo distinguir, pues de otro modo ya sería distinta.
- 2.024 La sustancia es aquello que independientemente de lo que acaece, existe.
- 2.025 Ella es forma y contenido.
- 2.0251 Espacio, tiempo y color (cromaticidad) son formas de los objetos.
- 2.026 Sólo si hay objetos puede haber una forma fija del mundo.
- 2.027 Lo fijo, lo existente y el objeto son uno.
- 2.0271 El objeto es lo fijo, lo existente; la configuración es lo cambiante, lo variable.
- 2.0272 La configuración de los objetos forma el hecho atómico.
- 2.03 En el hecho atómico los objetos depende unos de otros como los eslabones de una cadena.
- 2.031 En el hecho atómico los objetos están combinados de un modo determinado.
- 2.032 El modo en cómo los objetos depende unidos en el hecho atómico es la estructura del hecho atómico.
- 2.033 La forma es la posibilidad de la estructura.
- 2.034 La estructura del hecho consiste en la estructura del hecho atómico.
- 2.04 La totalidad de los hechos atómicos existentes es el mundo.
- 2.05 La totalidad de los hechos atómicos existentes determina también cuales hechos atómicos no existen.
- 2.06 La existencia y no-existencia de los hechos atómicos es la realidad (a la existencia de los hechos atómicos la llamamos también un hecho positivo, a la no-existencia, un hecho negativo)
- 2.061 Los hechos atómicos son independientes unos de otros.
- 2.062 De la existencia o no existencia de un hecho atómico, no se puede concluir la existencia o no existencia de otro.
- 2.063 La total realidad es el mundo.
- 2.1 Nosotros nos hacemos figuras de los hechos.
- 2.11 La figura Presenta los estados de cosas en el espacio lógico, la existencia y no-existencia de los hechos atómicos.
- 2.12 La figura es un modelo de la realidad.
- 2.13 A los objetos corresponden en la figura los elementos de la figura.
- 2.131 Los elementos de la figura están en la figura en lugar de los objetos.
- 2.14 La figura consiste en esto: en que sus elementos están combinados unos respecto de otros de un modo determinado.
- 2.141 La figura es un hecho.
- 2.15 Que los elementos de la figura estén combinados unos respecto de otros de un modo determinado, representa que las cosas están combinadas también unas respecto de otras. A esta conexión de los elementos de la figura se llama su estructura y a su posibilidad su forma de figuración.
- 2.151 La forma de la figuración es la posibilidad de que las cosas se combinen unas respecto de otras como los elementos de la figura.
- 2.1511 La figura estáis ligada en la realidad; llega hasta ella.
- 2.1512 Es como una escala aplicada a la realidad.
- 2.15121 Sólo los puntos extremos de la línea graduada tocan al objeto que ha de medirse.
- 2.1513 Según esta interpretación pertenece también a la figura la relación figurativa que hace de ella una figura.
- 2.1514 La relación figurativa consiste en la coordinación de los elementos de la figura y de las cosas.
- 2.1515 Estas coordinaciones son algo así como los tentáculos de los elementos de la figura con los cuales la figura toca la realidad.
- 2.16 Un hecho para poder ser figura, debe tener algo en común con lo figurado.
- 2.161 En la figura y en lo figurado debe haber algo idéntico para que una pueda ser figura de lo otro completamente.
- 2.17 Lo que la figura debe tener en común con la realidad para poder figurarla a su modo y manera –justa o falsamente- es su forma de figuración.
- 2.171 La figura puede figurar toda realidad de la cual tiene la forma. La figura espacial, todo lo que es espacial; la cromática, todo lo que es cromático.
- 2.172 La figura, sin embargo, no puede figurar su forma de figuración; la muestra.
- 2.173 La figura representa su objeto desde fuera (su punto de vista es su forma de representación), porque la figura representa su objeto, justa o falsamente.
- 2.174 La figura no puede sin embargo situarse fuera de su forma de representación.
- 2.18 Lo que cada figura, de cualquier forma, debe tener en común con la realidad para poderla figurar por completo –justa o falsamente- es la forma lógica, esto es, la forma de la realidad.
- 2.181 Si la forma de la figuración es la forma lógica, entonces a la figura se la llama lógica.
- 2.182 Toda figura es también una figura lógica (pero, al contrario, v.g., no toda figura es espacial).
- 2.19 La figura lógica puede figurar al mundo.
- 2.2 La figura tiene en común con lo figurado la forma lógica de figuración.
- 2.20
- 2.201 La figura figura la realidad representando una posibilidad de la existencia y de la no existencia de los hechos atómicos.
- 2.202 La figura representa un estado de cosas posible en el espacio lógico.
- 2.203 La figura contiene la posibilidad del estado de cosas que representa.
- 2.21 La figura concuerda con la realidad o no; es justa o equivocada, verdadera o falsa.
- 2.22 La figura representa lo que representa, independientemente de su verdad o falsedad, por medio de la forma de figuración.
- 2.221 Lo que la figura representa es su sentido.
- 2.222 En el acuerdo o desacuerdo de su sentido con la realidad, consiste su verdad o falsedad.
- 2.223 Para conocer si la figura es verdadera o falsa debemos compararla con la realidad.
- 2.224 No se puede conocer sólo por la figura si es verdadera o falsa.
- 2.225 No hay figura verdadera a priori.
 3 La figura lógica de los hechos es un pensamiento.
3 La figura lógica de los hechos es un pensamiento.- 3.0
- 3.00
- 3.001 «Un hecho atómico es pensable», significa: Nosotros podemos figurarlo.
- 3.01 La totalidad de los pensamientos verdaderos es una figura del mundo.
- 3.02 El pensamiento contiene la posibilidad del estado de cosas que piensa. Lo que es pensable también es posible.
- 3.03 Nosotros no podemos pensar nada ilógico, porque, de otro modo, tendríamos que pensar ilógicamente.
- 3.031 Se ha dicho alguna vez que Dios pudo crear todo salvo lo que fuese contrario a las leyes de la lógica. La verdad es que nosotros no somos capaces de decir qué aspecto tendría un mundo ilógico.
- 3.032 Presentar en el lenguaje algo que «contradiga a la lógica» es tan imposible como presentar en geometría por sus coordenadas un dibujo que contradiga a las leyes del espacio o dar las coordenadas de un punto que no existe.
- 3.0321 Podemos representarnos espacialmente un hecho atómico que contradiga las leyes de la física, pero no uno que contradiga a las leyes de la geometría.
- 3.04 Un pensamiento verdadero a priori sería aquel cuya posibilidad condicionase su verdad.
- 3.05 Sólo podríamos saber a priori que un pensamiento es verdadero si en el pensamiento mismo (sin objeto de comparación) se pudiese reconocer su verdad.
- 3.1 En la proposición, el pensamiento se expresa perceptiblemente por los sentidos.
- 3.11 Nosotros usamos el signo sensiblemente perceptible de la proposición (sonidos o signos escritos, etc.) como una proyección del estado de cosas posible. El método de proyección es el pensamiento del sentido de la proposición.
- 3.12 Llamo signo proposicional el signo mediante el cual expresamos el pensamiento. Y la proposición es el signo proposicional en su relación proyectiva con el mundo.
- 3.13 A la proposición pertenece todo aquello que pertenece a la proyección, pero no lo proyectado. O sea, la posibilidad de lo proyectado, pero no lo proyectado mismo. Pues en la proposición no está contenido su propio sentido, sino la posibilidad de expresarlo. («El contenido de la proposición» significa el contenido de la proposición con significado) En la proposición está contenida la forma de su sentido, pero no su contenido.
- 3.14 El signo proposicional consiste en esto: en que sus elementos, las palabras, están combinados de un modo determinado. El signo proposicional es un hecho.
- 3.141 La proposición no es una mezcla de palabras. (como el tema musical no es una mezcla de tonos). La proposición es articulada.
- 3.142 Sólo los hechos pueden expresar un sentido, una clase de nombres no puede.
- 3.143 Que el signo proposicional es un hecho, está oculto por la forma ordinaria de expresión escrita o impresa. Pues, por ejemplo, en la proposición impresa, el signo de la proposición no aparece como esencialmente diferente de la palabra. (Así fue posible que Frege definiese la proposición como un nombre compuesto.)
- 3.1431 La esencia del signo proposicional se hace muy clara cuando lo imaginamos compuesto de objetos espaciales (tales como mesas, sillas, libros) en vez de signos escritos. La recíproca posición espacial de estas cosas expresa el sentido de la proposición.
- 3.1432 No: «El signo complejo ‘aRb’ dice que ‘a’ está en la relación R con ‘b’», sino : Que ‘a’ está en una cierta relación con ‘b’, dice que ‘aRb’.
- 3.144 Los estados de cosas se pueden describir, pero no nombrar. (Los nombres son como puntos; las proposiciones, como flechas: tienen sentido.)
- 3.2 En las proposiciones, el pensamiento puede expresarse de modo que a los objetos del pensamiento correspondan los elementos del signo proposicional.
- 3.20
- 3.201 A estos elementos los llamo «signos simples» y a la proposición «completamente analizada».
- 3.202 Los signos simples empleados en la proposición se llaman nombres.
- 3.203 El nombre significa el objeto. El objeto es su significado. («A» es el mismo signo que «A».)
- 3.21 A la configuración de los signos simples en el signo proposicional corresponde la configuración de los objetos en el estado de cosas.
- 3.22 El nombre representa en la proposición al objeto.
- 3.221 A los objetos sólo los puedo nombrar. Los signos los representan. Yo solamente puedo hablar de ellos; no puedo expresarlos. Una proposición únicamente puede decir cómo es una cosa, no qué es una cosa.
- 3.23 El postulado de la posibilidad de los signos simples es el postulado de la determinidad del sentido.
3.24 La proposición que trata de un complejo está en relación interna con la proposición que trata de una de sus partes constitutivas.
El complejo sólo puede darse por descripción, y ésta será justa o errónea. La proposición en la cual se habla de un complejo no será, si éste no existe, sinsentido, sino simplemente falsa.
Que un elemento proposicional designa un complejo puede verse por una indeterminación en la proposición en la cal se encuentra. Nosotros sabemos que está ya todo determinado por esta proposición. (La notación de generalidad contiene un prototipo.)
La combinación de los símbolos de un complejo en un símbolo simple puede expresarse por una definición.
- 3.25 Hay un análisis completo, y sólo uno, de la proposición.
- 3.251 La proposición expresa lo que expresa de un modo determinado y claramente especificable: la proposición es articulada.
- 3.26 El nombre no puede ser subsecuentemente analizado por una definición. Es un signo primitivo.
- 3.261 Todo signo definido designa a través de aquellos signos por medio de los cuales fue definido; y la definición indica el camino. Dos signos, uno primitivo y otro definido mediante signos primitivos, no pueden designar del mismo modo y manera. Los nombres no pueden desmembrarse por definición. (Ningún signo por sí solo e independientemente tiene una definición.)
- 3.262 La aplicación del signo muestra lo que no está expresado en él. La aplicación muestra lo que el signo esconde.
- 3.263 El significado de los signos primitivos puede explicarse por elucidaciones. Elucidaciones son las proposiciones que contienen los signos primitivos. Estas sólo pueden, pues, ser comprendidas si los significados de estos signos son ya conocidos.
- 3.3 Sólo la proposición tiene sentido; sólo en el contexto de la proposición tiene el nombre significado.
- 3.31 Llamo una expresión (un símbolo) a cada una de las partes de la proposición que caracteriza su sentido. (La proposición misma es una expresión.) Expresión es todo aquello, esencial para el sentido de la proposición, que las proposiciones tienen en común unas con otras.
- 3.311 La expresión presupone la forma de todas las proposiciones en la cual puede encontrarse. Es la nota característica común de toda clase de proposiciones.
- 3.312 La expresión está representada por la forma general de las proposiciones a las cuales caracteriza. Y así en esta forma la expresión es constante y todo lo demás variable.
3.313 La expresión está, pues, representada por una variable cuyos valores son las proposiciones que contienen la expresión.
(En el caso límite, la variable se hace constante; la expresión, una proposición.)
Llamo a tal variable «variable proposicional».
3.314 La expresión tiene sólo significado en una proposición. Toda variable puede ser concebida como variable proposicional. (Incluyendo el nombre variable.)3.314 La expresión tiene sólo significado en una proposición. Toda variable puede ser concebida como variable proposicional. (Incluyendo el nombre variable.)
- 3.315 Si cambiamos una parte constitutiva de una proposición en una variable, hay una clase de proposiciones que son todos los valores de la proposición variable resultante. En general, esta clase depende también de lo que nosotros, por un acuerdo arbitrario, entendemos por parte de la proposición, pero si cambiamos en variables todos los signos cuyo significado había sido determinado arbitrariamente, entonces aún continúa habiendo una tal clase. Pero ésta ya no depende de ningún acuerdo, sino sólo de la naturaleza de la proposición. Corresponde a una forma lógica –a un prototipo lógico.
3.316 Cuáles valores pueda asumir la variable proposicional es algo determinado.
La determinación de los valores es la variable.
3.317 La determinación de los valores de la variable proposicional está dada por la indicación de las proposiciones, cuya nota común es la variable.
La determinación es una descripción de estas proposiciones.
La determinación trata, pues sólo de los símbolos, no de su significado.
Y sólo esto es esencial a la determinación: que sea sólo una descripción de los símbolos y no asevere nada acerca de lo designado.
El modo cómo se describa la proposición no es esencial.
- 3.318 Yo concibo la proposición como –Frege y Russell- como una función de las expresiones que contiene.
- 3.32 El signo es la parte del símbolo perceptible por los sentidos.
- 3.321 Dos símbolos diferentes pueden también tener en común el signo (el signo escrito o el signo oral). Los designan de diferente modo y manera.
- 3.322 No es nunca posible indicar la característica común de dos objetos designándolos con los mismos signos, por dos diferentes modos de designación. Pues el signo es arbitrario. Se puede también elegir dos signos diferentes. Pero entonces ¿dónde queda lo que era común en la designación?
3.323 En el lenguaje corriente ocurre muy a menudo que la misma palabra designe de modo y manera diferentes porque pertenezca a diferentes símbolos –o que dos palabras que designan de modo y manera diferentes se usen aparentemente del mismo modo en la proposición.
Así, la palabra «es» se presenta como cópula, como signo de igualdad y como expresión de la existencia; «existir», como un verbo intransitivo, lo mismo que «ir»; «idéntico», como adjetivo; hablamos de algo, pero también de que algo sucede.
(En la proposición «Verde es verde» - donde la primera palabra es un nombre propio y la última un adjetivo-, estas palabras no sólo tienen diferente significado, sino son también diferentes símbolos.)
- 3.324 Así nacen fácilmente las confusiones más fundamentales (de las cuales está llena toda la filosofía).
3.325 Para evitar estos errores debemos emplear un simbolismo que los excluya, no usando el mismo signo en símbolos diferentes ni usando aquellos signos que designen de modo diverso, de manera aparentemente igual. Un simbolismo, pues, que obedezca a la gramática lógica –a la sintaxis lógica.
(El simbolismo lógico de Frege y Russell es una tal simbolismo, aunque no exento aún de todo error.)
- 3.326 Para reconocer el símbolo en el signo debemos tener en cuenta si se usa con significado.
- 3.327 El signo determina una forma lógica sólo unido a su aplicación lógico-sintáctica.
3.328 Si un signo no es necesario carece de significado. Este es el sentido del principio de Ockam.
(Si todo funciona como si un signo tuviese in significado, entonces tiene un significado.)
- 3.33 En sintaxis lógica el significado de un signo no debe nunca desempeñar ningún papel; el significado debe poder establecerse sin que haya por ello que hablar del significado de un signo; debe solo presuponer la descripción de la expresión.
- 3.331 Esta observación nos permite ver más lejos en la «teoría de los tipos» de Russell. El error de Russell se manifiesta en esto: que Russell, para establecer las reglas de los signos, ha tenido necesidad de hablar del significado del signo.
- 3.332 Ninguna proposición puede decir nada de sí misma porque el signo proposicional no puede estar contenido en sí mismo (ésta es toda la «teoría de los tipos»).
3.333 Una función no puede ser su propio argumento porque el signo de la función contiene ya el prototipo de su propio argumento y no puede contenerse a sí mismo.
Si, por ejemplo, nosotros suponemos que la función F(fx) pudiera ser su propio argumento, entonces sería una proposición
«F(F(fx))», y en esta proposición la función externa F y la función interna F deberán tener diferentes significados, pues la interna tiene la forma Φ(fx), la externa, la forma φ(Φ(fx)).
Común a ambas funciones es tan sólo la letra «F», que por sí misma no significa nada.
Esto se hace más claro si en lugar de «F(F(u))» escribimos «(∃Φ):F(Φu).φu=Fu». Así describimos la paradoja de Russell.
- 3.334 Las reglas de la sintaxis lógica deben ser inteligibles por sí mismas con sólo conocer cómo cada signo designa.
3.34 La proposición posee aspectos esenciales y accidentales.
Accidentales son aquellos aspectos que se deben al particular modo de producir el signo proposicional. Esenciales son aquellos que sólo permiten a la proposición expresar su sentido.
- 3.341 Lo esencial en una proposición es aquello que es común a todas las proposiciones que pueden expresar el mismo sentido. Y del mismo modo, lo esencial, en general, a un símbolo es aquello que tienen en común todos los símbolos que pueden cumplir el mismo objeto.
- 3.3411 Se puede también decir: el verdadero nombre es aquello que tienen en común todos los símbolos que designan un objeto. De aquí se seguiría gradualmente que ninguna clase de composición es esencial para los nombres.
- 3.342 En nuestras notaciones hay, es cierto, algo de arbitrario; pero esto no es arbitrario, a saber: que si nosotros hemos determinado algo arbitrariamente, entonces algún algo debe acaecer. (Esto depende de la esencia de la notación.)
- 3.3421 Uno modo particular de designación puede carecer de importancia, pero siempre es importante que sea un posible modo de designación. Y así ocurre en general en filosofía: lo singular se manifiesta más y más inimportante; pero la posibilidad de cada singular nos ofrece una abertura sobre la esencia del mundo.
- 3.343 Las definiciones son reglas para traducir una lengua a otra. Cada simbolismo correcto debe ser traducible a cada uno de los otros de acuerdo con tales reglas. Esto es lo que todos tienen en común.
- 3.344 Lo que el símbolo designa es aquello que es común a todos aquellos símbolos por los cuales puede ser sustituido según las reglas de la sintaxis lógica.
3.3441 Se puede, por ejemplo, expresar del modo siguiente lo que es común a todas las notaciones de las funciones de verdad: tienen de común que todas ellas, por ejemplo, pueden ser sustituidas por la notación «~p» («no p») y «p v q» («p v q»).
(Con esto se indica el modo por el cual una posible notación especial puede darnos una información general.)
- 3.3442 El signo del complejo no se resuelve arbitrariamente en el análisis de tal modo que su resolución sea diferente en cada estructura proposicional.
- 3.4 La proposición determina un lugar en el espacio lógico. La existencia de este lugar lógico está garantizada sólo por la existencia de las partes constitutivas, por la existencia de la proposición con significado.
- 3.41 El signo proposicional y las coordenadas lógicas: esto es el lugar lógico.
- 3.411 El lugar geométrico y el lógico concuerdan en que ambos son la posibilidad de una existencia.
3.42 Aunque la proposición pueda sólo determinar un lugar en el espacio lógico, todo el espacio lógico debe estar dado por ella.
(De otro modo, la negación, la suma lógica, el producto lógico, etc., introducirían –en coordinación- siempre nuevos elementos.)
(El armazón lógico en torno a la figura determina el espacio lógico. La proposición atraviesa a todo el espacio lógico.)
- 3.5 El signo proposicional aplicado, pensado, es el pensamiento.
 4 El pensamiento es la proposición con significado.
4 El pensamiento es la proposición con significado.- 4.0
- 4.00
- 4.001 La totalidad de las proposiciones es el lenguaje.
4.002 El hombre posee la capacidad de construir lenguajes en los cuales todo sentido puede ser expresado sin tener una idea de cómo y qué significa cada palabra. Lo mismo que uno habla sin saber cómo se han producido los sonidos singulares.
El lenguaje corriente es una parte del organismo humano, y no menos complicada que él.
Es humanamente imposible captar inmediatamente la lógica del lenguaje.
El lenguaje disfraza el pensamiento. Y de tal modo, que por la forma externa del vestido no es posible concluir acerca de la forma del pensamiento disfrazado; porque la forma externa del vestido está construida con un fin completamente distinto que el de permitir reconocer la forma del cuerpo.
Los acomodamientos tácitos para comprender el lenguaje corriente son enormemente complicados.
4.003 La mayor parte de las proposiciones y cuestiones que se han escrito sobre materia filosófica no son falsas, sino sin sentido. No podemos, pues, responder a cuestiones de esta clase de ningún modo, sino solamente establecer su sinsentido.
La mayor parte de las cuestiones y proposiciones de los filósofos proceden de que no comprendemos la lógica de nuestro lenguaje.
(Son de esta clase las cuestiones de si lo bueno es más o menos idéntico que lo bello.)
No hay que asombrarse de que los más profundos problema no sean propiamente problemas.
4.0031 Toda la filosofía es «crítica del lenguaje» (pero no, en absoluto, en el sentido de Mauthner). Es mérito de Russell haber mostrado que la forma lógica aparente de la proposición no debe ser necesariamente su forma real.
- 4.01 La proposición es una figura de la realidad. La proposición es un modelo de la realidad tal como la pensamos.
4.011 A primera vista no parece que la proposición –tal como está impresa en el papel- sea una figura de la realidad de la que trata. Tampoco la notación musical parece a primera vista una figura de la música, ni nuestra escritura fonética (las letras) parece una figura de nuestro lenguaje hablado.
Sin embargo, estos símbolos demuestran, bien que en el sentido ordinario de la palabra, que son figuras de lo que representan.
- 4.012 Es claro que nosotros percibimos una proposición de la forma «aRb» como figura. Aquí el signo es claramente un trasunto del significado.
4.013 Y si penetramos la esencia de esta figuratividad veremos que no está perturbada por irregularidades aparentes (como el uso del # y del b en la notación musical).
Porque también estas irregularidades figuran aquello que deben expresar; pero de modo y manera distintos.
4.014 El disco gramofónico, el pensamiento musical, la notación musical, las ondas sonoras, están todos, unos respecto de otros, en aquella interna relación figurativa que se mantiene entre el lenguaje y el mundo.
A todo esto es común la estructura lógica. (Como en la fábula, los dos jóvenes, sus dos caballos y sus lirios son todos, en cierto sentido, la misma cosa.)
- 4.0141 La íntima semejanza entre estas cosas, aparentemente tan distintas, consiste en que hay una regla general mediante la cual el músico es capaz de leer la sinfonía en la partitura y por la cual se puede reconstruir la sinfonía grabándola en un disco gramofónico, y de este modo, por medio de la regla primera, llegar de nuevo a la partitura. Tal regla es la ley de la proyección que proyecta la sinfonía en el lenguaje de la notación musical. Es la regla de la traducción del lenguaje de la notación musical al lenguaje del disco.
- 4.015 La posibilidad de todos nuestros trasuntos, de toda la figuratividad de nuestros medios de expresión, descansa en la lógica de la figuración.
- 4.016 Para comprender la esencia de la proposición, pensemos en la escritura jeroglífica, que figura los hechos que describe. Y de ella, sin perder la esencia de la figuración, proviene la escritura alfabética.
- 4.02 Y así vemos que nosotros comprendemos el sentido del signo proposicional, sin que nos sea explicado.
- 4.021 La proposición es una figura de la realidad, pues yo conozco el estado de cosas que representa si yo entiendo el sentido de la proposición. Y yo entiendo la proposición sin que me haya sido explicado su sentido.
- 4.022 La proposición muestra su sentido. La proposición, si es verdadera, muestra cómo están las cosas. Y dice que las cosas están así.
4.023 La realidad debe ser fijada por la proposición en sí o en no.
Por esto debe ser completamente descrita por ella.
La proposición es la descripción de un hecho atómico.
Lo mismo que la descripción de un objeto lo describe según sus propiedades externas, así la proposición describe la realidad según sus internas propiedades.
La proposición construye un mundo con la ayuda de un armazón lógico; por ello es posible ver en la proposición, si es verdadera, el aspecto lógico de la realidad. Se pueden obtener conclusiones de una falsa proposición.
4.024 Entender una proposición quiere decir, si es verdadera, saber lo que acaece.
(Se puede también entenderla sin saber, si es verdadera.)
Se la entiende cuando se entienden sus partes constitutivas.
4.025 La traducción de una lengua a otra no es un proceso de traducción de cada proposición a otra proposición, sino sólo la traducción de las partes constitutivas de las proposiciones.
(Y el diccionario no traduce sólo los substantivos, sino también los adverbios, conjunciones, etc.; y trata todo del mismo modo.)
4.026 La significación de los signos simples (las palabras) debe sernos explicada para que los comprendamos.
Pero nosotros nos entendemos con las proposiciones.
- 4.027 Yace en la esencia de la proposición que pueda comunicarnos un nuevo sentido.
4.03 Una proposición debe comunicar con expresiones viejas un sentido nuevo.
La proposición que nos comunica un estado de cosas debe estar también esencialmente conectada con el estado de cosas.
Y la conexión consiste, precisamente, en que es su figura lógica.
La proposición sólo dice algo en cuanto es una figura.
4.031 En la proposición viene, por así decirlo, construido, en conjunto, un estado de cosas a modo de experimento.
Uno puede decir en lugar de esta proposición tiene tal y tal sentido, esta proposición representa tal y tal estado de cosas.
- 4.0311 Un nombre está en lugar de una cosa y otro en lugar de otra y están unidos entre sí. Así el todo representa –como una figura viva- el hecho atómico.
4.0312 La posibilidad de la proposición descansa en el principio de la representación de los objetos por los signos.
Mi pensamiento fundamental es que «las constantes lógicas» no representan. Que la lógica de los hechos no puede ser representada.
4.032 La proposición es una figura de un estado de cosas sólo en cuanto está lógicamente organizada.
(También la proposición «ambulo» es compuesta, pues su raíz da un sentido diferente con otra terminación, o si la terminación se une con otra raíz.
- 4.04 En la proposición deben distinguirse tantas cosas cuantas hay en el estado de cosas que representa. Ambas deben poseer la misma multiplicidad lógica (matemática). (Cf. la mecánica de Hertz a propósito de los modelos dinámicos.)
- 4.041 Esta multiplicidad matemática no puede, naturalmente, ser a su vez figurada. De ella no se puede salir por la figuración.
4.0411 Si nosotros queremos, por ejemplo, expresar lo que se expresa por «(x) . fx», anteponiendo un índice delante de «fx», como: «Gen. fx», esto no sería suficiente porque no sabríamos qué era lo generalizado. Si quisiéramos indicarlo por un índice «g», como: «f(x subg)», no sería suficiente – pues desconoceríamos el campo de la generalización.
Si quisiéramos intentarlo por la introducción de un signo en el lugar de argumento, como «(G,G) . F(G,G)», tampoco bastaría, pues no podríamos determinar la identidad de las variables. Etc.
Todos estos modos de simbolización son insuficientes porque no poseen la multiplicidad matemática necesaria.
- 4.0412 Por la misma razón no es suficiente la explicación idealista de la visualidad de las relaciones espaciales por «anteojos espaciales» porque esto no explica la multiplicidad de estas relaciones.
- 4.05 La realidad es comparada con la proposición.
- 4.06 La proposición puede ser verdadera o falsa sólo en cuanto es una figura de la realidad.
4.061 Si no consideramos que la proposición tiene un sentido independiente de los hechos, podemos creer fácilmente que verdadero y falso son relaciones del mismo orden entre signo y designado.
Se podría, por ejemplo, decir que «p» designa de modo verdadero lo que «~p» designa de modo falso, etc.
- 4.062 ¿No podríamos entendernos por medio de proposiciones falsas, hast tanto que supiéramos que tenían un significado falso? ¡No! Porque una proposición es verdadera cuando nosotros decimos por medio de ella lo que acaece ; y si nosotros por «p» significamos ~p, y lo que significamos es lo que acaece, entonces «p» es, en la nueva concepción, verdadero y no falso.
- 4.0621 Pero es importante que los signos «p» y «~p» puedan decir lo mismo. Pues esto indica que nada corresponde en la realidad al signo «~». Que en una proposición entre una negación no es característico de su sentido (~ ~p=p) las preposiciones «p» y «~p» tienen sentido opuesto, pero les corresponde una y la misma realidad.
4.063 Un ejemplo para aclarar el concepto de verdad. Sobre un papel blanco hay una mancha negra; la forma de la mancha puede describirse diciendo de cada uno de los puntos de la superficie si es blanco o negro. Al hecho de que un punto sea negro, corresponde un hecho positivo; al hecho de que un punto sea blanco (no negro), un hecho negativo. Si yo designo un punto de la superficie (un valor de verdad en la terminología de Frege) esto corresponde a la hipótesis que se había propuesto para ser juzgada.
Pero para poder decir que un punto es negro o blanco, yo debo previamente saber en qué condiciones se llama a un unto negro y cuáles blanco; y para poder decir:
«p» es verdadero (o falso), debo haber determinado en qué condiciones llamo verdadero a «p» y con ello determino el sentido de la proposición.
El punto en el cual el parangón se rompe es éste: Nosotros podemos indicar un punto del papel sin saber qué cosa sea blanco y qué negro; pero a una proposición sin sentido no corresponde nada en absoluto, ya que no designa ninguna cosa (valor de verdad) cuyas propiedades se llamen falsas o verdaderas; el verbo de una proposición no es –como creía Frege- «es verdadero» o «es falso», sino que aquello que «es verdadero» debe contener ya al verbo.
- 4.064 Cada proposición debe ya tener un sentido; la aseveración no puede dárselo, pues lo que asevera es el sentido mismo. Y lo mismo vale para la negación, etc.
4.0641 Se puede decir: la negación está ya referida al lugar lógico determinado por la proposición denegada. La proposición que niega determina otro lugar lógico que el de la proposición negada. La proposición que niega determina un lugar lógico con ayuda del lugar lógico de la proposición negada, describiendo a aquél como estando fuera de éste.
Que la proposición que niega pueda ser de nuevo negada indica que lo que es negado es ya una proposición y no meramente la preparación de una proposición.
- 4.1 Una proposición representa la existencia y no existencia de los hechos atómicos.
- 4.11 La totalidad de las proposiciones verdaderas es la ciencia natural total (o la totalidad de las ciencias naturales).
4.111 La filosofía no es una de las ciencias naturales.
(La palabra «filosofía» debe significar algo que esté sobre o bajo, pero no junto a las ciencias naturales.)
4.112 El objeto de la filosofía es la aclaración lógica del pensamiento.
Filosofía no es una teoría, sino una actividad.
Una obra filosófica consiste esencialmente en elucidaciones.
El resultado de la filosofía no son «proposiciones filosóficas», sino el esclarecerse de las proposiciones.
La filosofía debe esclarecer y delimitar con precisión los pensamientos que de otro modo serían, por así decirlo, opacos y confusos.
- 4.1121 La psicología no es más afín a la filosofía que cualquier otra ciencia natural. La teoría del conocimiento es la psicología de la filosofía. ¿No corresponde mi estudio del signo-lenguaje al estudio del proceso mental que los filósofos sostenían que era esencial a la filosofía de la lógica? Sólo así se han perdido los más en investigaciones psicológicas no esenciales. E incluso mi método corre análogo peligro.
- 4.1122 La teoría de Darwin no tiene mayor relación con la filosofía que cualquiera otra de las hipótesis de la ciencia natural.
- 4.113 La filosofía delimita el campo disputable de las ciencias naturales.
4.114 Debe delimitar lo pensable y con ello lo impensable.
Debe delimitar lo impensable desde el centro de lo pensable.
- 4.115 Significará lo indecible presentando claramente lo decible.
- 4.116 Todo aquello que puede ser pensado, puede ser pensado claramente. Todo aquello que puede ser expresado, puede ser expresado claramente.
- 4.12 La proposición puede representar toda la realidad, pero no puede representar lo que debe tener de común con la realidad para poder representar –la forma lógica. Y para poder representar la forma lógica debemos poder colocarnos con la proposición fuera de la lógica; es decir fuera del mundo.
4.121 La proposición no puede representar la forma lógica, se refleja en ella.
Lo que en el lenguaje se refleja, nosotros no podemos expresarlo por el lenguaje.
La proposición muestra la forma lógica de la realidad.
La exhibe.
4.1211 Así, una proposición «fa» muestra que entra en su sentido el objeto a; dos proposiciones «fa» y «ga» muestran que en ambos se habla del mismo objeto.
Si dos proposiciones contradicen una a la otra, esto se muestra así en su estructura; lo mismo si una sigue a la otra, etc.
- 4.1212 Lo que se puede mostrar no puede decirse.
- 4.1213 Ahora podemos comprender porqué nos sentimos en posesión de una forma lógica exacta sólo cuando en nuestro simbolismo todo va bien.
4.122 Nosotros podemos hablar en cierto sentido de las propiedades formales de los objetos y de los hechos atómicos, o de las propiedades de la estructura de los hechos, y, en el mismo sentido, de relaciones formales y de relaciones de estructura.
(En vez de propiedad de estructura digo también «propiedad interna»; en vez de relación de estructura digo «relación interna».)
Introduzco estas expresiones para mostrar la razón de la confusión, tan extendida entre los filósofos, entre relaciones internas y relaciones propias (externas).
La existencia de tales propiedades y relaciones internas no puede, sin embargo, ser aseverada por las proposiciones, sino que se muestra en las proposiciones que representan los hechos atómicos y tratan de los objetos en cuestión.
- 4.1221 A una propiedad interna de un hecho podemos llamarla un rasgo de este hecho. (En el sentido en que hablamos de los rasgos del rostro.)
4.123 Una propiedad es interna cuando es impensable que su objeto no la posea.
(Este color azul y aquel color azul están eo ipso en la relación interna de más claro y más oscuro. Es impensable que estos dos objetos no estén en esta relación.)
(Aquí el uso oscilante de las palabras «propiedad» y «relación» corresponde el uso oscilante de la palabra «objeto».)
4.124 La existencia de una propiedad interna de un posible estado de cosas no viene expresada por una proposición, pero se expresa por sí en la proposición que representa el estado de cosas, mediante una propiedad interna de esta proposición.
Sería tan sinsentido atribuir una propiedad formal a una proposición, como negársela.
- 4.1241 No se pueden distinguir unas formas de otras diciendo que una tiene esta propiedad, y la otra, otra; porque esto presupone que hay un sentido en aseverar ambas propiedades de ambas formas.
- 4.125 La existencia de las relaciones internas entre posibles estados de cosas se expresa en el lenguaje corriente por una relación interna entre las proposiciones que las representan.
- 4.1251 Así se resuelve la controversia sobre «si todas las relaciones son internas o externas».
4.1252 Llamo series formales a aquellas que están ordenadas por relaciones internas.
La serie de los números no está ordenada por una relación externa, sino interna.
Asimismo la serie de las proposiciones
«aRb».
«(∃ x): aRx.xRb»,
«(∃ x,y): aRx.xRy.yRb», etc.
(Si b está en una de estas relaciones con a, yo llamo a b sucesor de a.)
4.126 En el sentido en que nosotros hablamos de propiedades formales, podemos hablar ahora también de conceptos formales.
(Introduzco esta expresión para esclarecer la razón de la confusión entre conceptos formales y conceptos propios que ha impregnado a toda la vieja lógica.)
Que algo caiga bajo un concepto formal como su objeto, no se puede expresar por una proposición. Pero esto se muestra en el símbolo del objeto mismo. (El nombre muestra que él significa un objeto; el signo numérico, que él significa un número, etc.)
El concepto formal no puede representarse por una función como se hace con los conceptos propios.
Por sus características, las propiedades formales no pueden ser expresadas por funciones.
La expresión de una propiedad formal es un rasgo de ciertos símbolos.
El signo de las características de un concepto formal es, pues, un rasgo característico de todos los símbolos cuyos significados caen bajo el concepto.
La expresión de un concepto formal es, pues, una variable proposicional en la cual sólo es constante este rasgo característico.
- 4.127 La variable proposicional designa el concepto formal, y sus valores designan los objetos que caen bajo esto concepto formal. Toda variable es el signo de un concepto formal.
- 4.1271 Toda variable representa una forma constante que todos sus valores poseen y que puede ser concebida como propiedad formal de estos valores.
4.1272 Así, el nombre variable «x» es el signo propio del pseudo-concepto objeto.
Siempre que la palabra «objeto» («cosa», «entidad», etc.) se use correctamente, está expresada en el simbolismo lógico por el nombre variable. Por ejemplo, en la proposición «hay dos objetos que…» por «(∃x,y)...».
Así, por ejemplo, no se puede decir «hay objetos», como se dice «hay libros». Y tampoco se puede decir «hay cien objetos» o «hay ‘x’ objetos».
Y no tiene sentido hablar del número de todos los objetos.
Lo mismo vale para las palabras «complejo», «hecho», «función», «número», etc.
Todas ellas designan conceptos formales, y se representan en el simbolismo lógico por variables, no por funciones o clases. (Como Frege y Russell creen.)
Expresiones como «1 es un número», «hay sólo un cero», y todas otras semejantes, son un sinsentido.
(Es tan sin sentido decir «hay sólo 1» como decir 2+2 es a las 3 en punto igual a 4.)
- 4.12721 El concepto formal está ya dado con el objeto que cae bajo él. No se puede, pues, introducir como idea primitiva los objetos que caen bajo un concepto formal y el concepto formal mismo. No se puede, pues, por ejemplo, introducir (como Russell hace) el concepto de función y también las funciones especiales como ideas primitivas: o el concepto de número y números determinados.
4.1273 Si queremos expresar en el simbolismo lógico la proposición general «b es un sucesor de a», necesitaremos una expresión para el término general de la serie formal: aRb, (∃x):aRx.xRb, (∃x,y): aRx.xRy.yRb,... El término general de una serie formal sólo puede expresarse por una variable, pues el concepto «término de esta serie formal» es un concepto formal. (Esto se les ha escapado a Frege y a Russell; el modo con que ellos expresan las proposiciones generales, como la antedicha, es falso; contiene un círculo vicioso.)
Podemos determinar el término general de la serie formal dando su primer término y la forma general de la operación que produce el término sucesivo de la proposición precedente.
4.1274 La cuestión acerca de la existencia de un concepto formal es un sinsentido, pues ninguna proposición puede responder a tal cuestión.
(Por ejemplo, no podemos preguntar: «¿Hay proposiciones de sujeto predicado inanalizables?»
4.128 Las formas lógicas son anuméricas.
No hay pues, en lógica números privilegiados, no hay tampoco ningún monismo o dualismo filosófico, etc.
- 4.2 El sentido de la proposición es su acuerdo o desacuerdo con las posibilidades de existencia y no existencia del hecho atómico.
- 4.21 La proposición más simple, la proposición elemental, afirma la existencia de un hecho atómico.
- 4.211 Un signo característico de las proposiciones elementales es que ninguna proposición elemental puede estar en contradicción con ella.
- 4.22 La proposición elemental consta de nombres. Es una conexión, una concatenación de nombres.
4.221 Es patente que en el análisis de las proposiciones debemos llegar a proposiciones elementales, las cuales constan de nombres en unión inmediata.
Surge aquí la cuestión de cómo puede llegar a realizarse la conexión proposicional.
- 4.2211 Aunque el mundo fuese infinitamente complejo, de modo que cada hecho constase de infinidad de hechos atómicos, y cada hecho atómico se compusiese de un número infinito de objetos, incluso en este supuesto debería haber objetos y hechos atómi cos.
- 4.23 El nombre se encuentra en la proposición sólo en el contexto de la proposición elemental.
4.24 Los nombres son los símbolos simples; yo los designo con letras particulares («x», «y», «z»).
La proposición elemental la escribo como función del nombre, en la forma «fx», «φ(x,y)», etcétera.
O también las designo por las letras p, q, r.
4.241 Si yo uso los signos con uno y el mismo significado, lo expreso poniendo entre los dos el signo «=».
«a=b» significa, pues, que el signo «a» es reemplazable por el signo «b».
(Si yo introduzco por una ecuación un nuevo signo «b» para determinar que debe sustituir un signo «x» ya conocido, escribo (como Russell) la ecuación –definición- en la forma: «a=b def.». La definición es una regla simbólica.
- 4.242 Expresiones de la forma «a=b» son pues, tan sólo recursos de la representación: no dicen nada sobre el significado de los signos «a» y «b».
4.243 ¿Podíamos entender dos nombres sin saber si designan la misma cosa o dos cosas diversas? ¿Podíamos entender una proposición en la que entren dos nombres sin saber si éstos significan la misma cosa o cosas diferentes?
Si yo conozco el significado de una palabra inglesa y de la correspondiente palabra alemana, es imposible que no sepa que tienen el mismo significado, es imposible que no sepa traducir la una en la otra.
Expresiones como «a=a», u otras derivadas de ellas, no son ni proposiciones elementales ni signos con significado. (Esto lo señalaremos más tarde.)
- 4.25 Si la proposición elemental es verdadera, el hecho atómico existe; si es falsa, el hecho atómico no existe.
- 4.26 La enumeración de todas las proposiciones elementales verdaderas describe el mundo completamente. El mundo está completamente descrito por la especificación de todas las proposiciones elementales más la indicación de cuáles son verdaderas y cuáles falsas.
4.27 Con relación a la existencia de n hechos atómicos hay
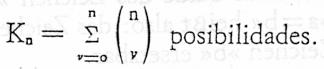
Es posible para todas las combinaciones de hechos atómicos existir, y a las otras no existir.
- 4.28 A estas combinaciones corresponde el mismo número de posibilidades de verdad –y de falsedad- de n proposiciones elementales.
- 4.3 La posibilidad de verdad de las proposiciones elementales significa las posibilidades de existencia y de no existencia de los hechos atómicos.
4.31 Las posibilidades de verdad pueden ser representadas por esquemas de la siguiente clase («V» significa «verdadero», «F» significa «falso». La serie de «V» y de «F» bajo la serie de las proposiciones elementales significan, en un simbolismo fácilmente inteligible, sus posibilidades de verdad):
p q r V V V F V V V F V V V F F F V F V F V F F F F F p q V V F V V F F F p V F
- 4.4 La proposición es la expresión del acuerdo y desacuerdo con la posibilidad de verdad y falsedad de las proposiciones elementales.
- 4.41 Las posibilidades de verdad de las proposiciones elementales son las condiciones de la verdad y falsedad de las proposiciones.
- 4.411 Parece probable a primera vista que la introducción de las proposiciones elementales sea fundamental para la comprensión de todas la otras clases de proposiciones. En efecto, la comprensión de las proposiciones generales depende sensiblemente de las proposiciones elementales.
4.42 Respecto del acuerdo y desacuerdo de una proposición con las posibilidades de verdad de n proposiciones fundamentales, hay
4.43 Podríamos Expresar el acuerdo con las posibilidades de verdad coordinando con ellas, en el esquema, el signo «V» (verdadero).
La ausencia de tal signo indica el desacuerdo.
4.431 La expresión de acuerdo y desacuerdo con las posibilidades de verdad de las proposiciones elementales, expresa las condiciones de verdad de la proposición.
La proposición es la expresión de sus condiciones de verdad.
(Con toda razón, Frege la ha puesto al comienzo como aclaración de los signos de su simbolismo lógico. Sólo es falsa en Frege la explicación del concepto de verdad: si lo «verdadero» y lo «falso» fuesen realmente objetos y argumentos en ~p, etc., entonces el sentido de «~p» no estaría, según la determinación de Frege, efectivamente determinado.)
- 4.44 El signo que surge de la coordinación del signo «V» con las posibilidades de verdad, es un signo proposicional.
4.441 Es claro que al complejo de los signos «V» y «F» no corresponde ningún objeto (o complejo de objetos), lo mismo que no corresponde a las líneas verticales y horizontales o a los paréntesis. No hay «objetos lógicos».
Lo mismo vale, naturalmente, para todos los signos que expresan lo mismo como los esquemas de «V» y «F».
4.442 Esto es, por ejemplo, un signo proposicional.
p q V V V >> F V V << V F F F V (El signo «aseverativo» de Frege «|-» carece lógicamente, por entero, de significado; indica sólo en Frege (y en Russell) que estos autores tienen por verdaderas las proposiciones que llevan este signo «|-», que pertenece, pues a la proposición tan poco como el número de orden de ésta. Es imposible que una proposición pueda afirmar de sí misma que es verdadera.)
Si la consecuencia de las posibilidades de verdad en el esquema está determinada, de una vez para siempre, por una regla de combinación, entonces la última columna es por sí misma una expresión de las condiciones de verdad. Si escribimos tal columna como una serie, el signo proposicional será: «(VV-V) (p, q)», o más claramente «(VVFV) (p, q)». El número de sitios en el paréntesis de la izquierda está determinado por el número de términos en el de la derecha.)
4.45 Para n proposiciones elementales se dan L subn grupos posibles de condiciones de verdad.
Los grupos de condiciones de verdad que pertenecen a las posibilidades de verdad de un número de proposiciones elementales pueden ordenarse en una serie.
4.46 Entre los posibles grupos de condiciones de verdad, hay dos casos extremos.
En uno la proposición es verdadera para todas las posibilidades de verdad de las proposiciones elementales. Nosotros decimos que las condiciones de verdad son tautológicas.
En el otro caso la proposición es falsa para todas las posibilidades de verdad: las condiciones de verdad son contradictorias.
En el primer caso llamamos a la proposición una tautología, en el segundo caso una contradicción.
4.461 La proposición muestra aquello que dice; la tautología y la contradicción muestran que no dicen nada.
La tautología no tienen condiciones de verdad, pues es incondicionalmente verdadera; y la contradicción, bajo ninguna condición es verdadera.
La tautología y la contradicción carecen de sentido.
(Como el punto del cual parten dos flechas en direcciones opuestas.)
(Yo no sé, por ejemplo, nada sobre el tiempo, cuando yo sé que llueve o no llueve.)
- 4.4611 Tautología y contradicción no son, sin embargo, sinsentidos; pertenecen al simbolismo, del mismo modo que «0» pertenece al simbolismo de la aritmética.
- 4.462 Tautología y contradicción no son figuras de la realidad. No representan ningún posible estado de cosas. En efecto, una permite todos los posibles estados de cosas; la otra, ninguno. En la tautología, las condiciones de acuerdo con el mundo –las relaciones representativas- se anulan recíprocamente en cuanto no están en ninguna relación representativa de la realidad.
4.463 Las condiciones de verdad determinan el campo que la proposición deja libre a los hechos.
(La proposición, la figura, el modelo, son en sentido negativo como un cuerpo sólido que limita el libre movimiento de los otros; en sentido positivo, como el espacio limitado por una sustancia sólida en la cual el cuerpo tiene su sitio.)
La tautología deja a la realidad todo el espacio lógico –infinito-; la contradicción llena todo el espacio lógico y no deja a la realidad ni un punto. Ninguna de las dos pueden, pues, determinar de ningún modo a la realidad.
4.464 La verdad de la tautología es cierta; la de las proposiciones, posible; la de las contradicciones, imposible.
(Cierto, posible, imposible: aquí tenemos la indicación de aquella gradación de la que tenemos necesidad en la teoría de la probabilidad)
- 4.465 El producto lógico de una tautología y de una proposición dice lo mismo que la proposición. Así, pues, tal producto es idéntico con la proposición. Pues no es posible alterar la esencia del símbolo sin alterar su sentido.
4.466 A una determinada unión lógica de signos corresponde una determinada unión lógica de sus significados: cada unión arbitraria corresponde sólo a signos no unidos.
Esto es, que las proposiciones que son verdaderas para cada estado de cosas no pueden de ningún modo ser uniones de signos, porque si no, sólo podrían corresponderlas uniones determinadas de objetos. (Y a una unión no lógica no corresponde ninguna unión de objetos.)
Tautología y contradicción son los casos límite de la unión de signos, es decir, su disolución.
- 4.4661 Naturalmente, los signos están también unidos unos con otros en la tautología y contradicción; es decir, están en relación unos con otros; pero estas relaciones carecen de significado, son inesenciales al símbolo.
4.5 Ahora parece posible dar la forma más general de la proposición; es decir, dar una descripción de las proposición; es decir, dar una descripción de las proposiciones de un simbolismo cualquiera, y también que todo sentido posible pueda expresarse por un símbolo que caiga bajo la descripción, y, por otra parte, que todo símbolo que caiga bajo la descripción pueda expresar un sentido si el significado de los nombres ha sido elegido en correspondencia.
Es claro que en la descripción de la forma más general de la proposición, solo puede ser descrito lo que le es esencial – de otro modo no sería la forma más general.
Que hay una forma general de la proposición se prueba por el hecho de que no pueda darse ninguna proposición cuya forma no se haya podido prever (es decir, construir). La forma general de la proposición es: tal y tal es lo que acaece.
- 4.51 Supongamos que se me dan todas las proposiciones elementales: entonces se puede preguntar simplemente: ¿qué proposiciones podría yo formar con ellas? Y éstas son todas las proposiciones y así están delimitadas.
- 4.52 Las proposiciones son todo aquello que se sigue de la totalidad de todas las proposiciones elementales. (Naturalmente, también del hecho de que es la totalidad de todas.) (Así podría decirse, en cierto sentido, que todas las proposiciones son generalizaciones de las proposiciones elementales.)
- 4.53 La forma general de la proposición es una variable.

5 La proposición es un valor de verdad de la proposición elemental.
(La proposición elemental es una función de verdad de sí misma.)
- 5.0
- 5.01 Las proposiciones elementales son los argumentos de verdad de las proposiciones.
5.02 Es fácil confundir los argumentos de función con los índices de nombres. En efecto, tanto por el argumento como por el índice se reconoce el significado del signo que le contiene.
Así, por ejemplo, en «+c» de Russell, «c» es un índice que indica que el signo entero es el signo de adición para los números cardinales. Pero esta designación depende de un acuerdo arbitrario y se puede, pues, elegir un signo simple en vez de «+c». pero en «~p» «p» no es un índice, sino un argumento; el sentido de «~p» no puede entenderse si no se ha entendido previamente el sentido de «p». (En el nombre de Julio César, «Julio» es un índice. El índice es siempre parte de una descripción del objeto, a cuyo nombre va unido. Por ejemplo, el César de la familia Julia.)
La confusión entre argumento e índice está a la base, si no estoy en un error, de la teoría de Frege sobre el significado de las proposiciones y de las funciones. Para Frege, las proposiciones de la lógica serían nombres, y sus argumentos, los índices de estos nombres.
5.1 Las funciones de verdad se pueden ordenar en series.
Este es el fundamento de la teoría de la probabilidad.
- 5.10
5.101 Las funciones de verdad de cualquier número de proposiciones elementales, pueden escribirse en un esquema del tipo siguiente:
(VVVV)(p,q) Tautología (Si p entonces p, y si q entonces q) (p ɔ p . q ɔ q) (FVVV)(p, q) en palabras: No ambas p y q (~(p . q)) (VFVV)(p, q) en palabras: Si q entonces p (q ɔ p) (VVFV)(p, q) en palabras: Si p entonces q (p ɔ q) (VVVF)(p, q) en palabras: p ó q (p C q) (FFVV)(p, q) en palabras: No q (~q) (FVFV)(p, q) en palabras: No p (~p) (FVVF)(p, q) en palabras: p ó q, pero no ambas (p.~q : v : q.~p) (VFFV)(p, q) en palabras: Si p entonces q, y si q entonces p (p≡q) (VFVF)(p, q) en palabras: p (VVFF)(p, q) en palabras: q (FFFV)(p, q) en palabras: Ni p ni q (~p.~q) ó (p | q) (FFVF)(p, q) en palabras: p y no q (p.~q) (FVFF)(p, q) en palabras: q y no p (q.~p) (VFFF)(p, q) en palabras: q y p (q.p) (FFFF)(p, q) Contradicción (p y no p, q y no q) (p.~p.q.~q) A aquellas posibilidades de verdad de sus argumentos de verdad que verifican la proposición, los llamo fundamentos de la verdad.
- 5.11 Si los fundamentos de verdad que son comunes a un número de proposiciones son también todos los fundamentos de verdad de una cierta proposición se sigue de la verdad de aquellas proposiciones.
- 5.12 En particular, la verdad de una proposición «p» se sigue de la verdad de otra proposición «q», si todos los fundamentos de verdad de la segunda son fundamentos de verdad de la primera.
- 5.121 Los fundamentos de verdad de una están contenidos en los de otra; p se sigue de q.
- 5.122 Si p se sigue de q, el sentido de «p» se sigue de «q».
- 5.123 Si un Dios crea un mundo en el cual ciertas proposiciones son verdaderas, crea también un mundo en el cual todas las proposiciones que derivan de ellas son verdaderas. Y de modo semejante, no puede crear un mundo en el cual la proposición «p» sea verdadera sin crear todos sus objetos.
- 5.124 Una proposición asevera toda proposición que se siga de ella.
5.1241 «p·q» es una de las proposiciones que aseveran «p» y al mismo tiempo una de la proposiciones que aseveran «q».
Dos proposiciones son opuestas entre sí si no hay una proposición con significado que asevera a ambas.
Toda proposición que contradice a otra la niega.
- 5.13 Que la verdad de una proposición se siga de la verdad de otra proposición lo percibimos por la estructura de las proposiciones.
- 5.131 Si la verdad de una proposición se sigue de la verdad de otra, esto se expresa por las relaciones en que están, unas respecto de otras, las formas de las proposiciones; y no es necesario que las pongamos en estas relaciones uniéndolas entre sí en una proposición. Pues estas relaciones son internas y existen.
5.1311 Si concluimos de pvq y ~p a q, la relación entre las formas de las proposiciones «pvq» y «~p» queda oculta por el modo de designación. Pero si escribimos, por ejemplo, en vez de «pvq» «p|q.|.p|q» y en vez de «~p» «p|p» (p|q=ni p ni q), entonces la conexión interna resulta obvia.
(Que de (x).fx se pueda concluir fa muestra que la generalidad está también presente en el símbolo «(x).fx».)
5.132 Si p se sigue de q yo puedo concluir de q a p; inferir p de q.
El modo de inferencia se obtiene sólo de las dos proposiciones.
Sólo las dos proposiciones pueden justificar la inferencia.
«Leyes de inferencia» que –como en Frege y Russell- hayan de justificar la inferencia, no tienen sentido y son superfluas.
- 5.133 Toda inferencia es a priori.
- 5.134 De una proposición elemental no se puede inferir ninguna otra.
- 5.135 De ningún modo es posible inferir de la existencia de un estado de cosas la existencia de otro estado de cosas enteramente diferente de aquél.
- 5.136 No existe un nexo causal que justifique tal inferencia.
5.1361 No podemos inferir los acontecimientos futuros de los presentes.
La fe en el nexo causal es la superstición.
5.1362 La libertad de la voluntad consiste en que no podemos conocer ahora las acciones futuras. Sólo podríamos conocerlas si la causalidad fuese una necesidad interna, la necesidad de la conclusión lógica. La conexión entre conocer y conocido es la de la necesidad lógica.
(«A conoce que p acaece» no tiene sentido si p es una tautología.)
- 5.1363 Lo mismo que del hecho de que una proposición nos sea evidente, no se sigue que sea verdadera, del mismo modo la evidencia no justifica nuestra creencia en su verdad.
- 5.14 Si una proposición se sigue de otra, la última dice más que la primera, la primera menos que la última.
- 5.141 Si p deriva de q y q de p son una y la misma proposición.
- 5.142 La tautología se sigue de todas las proposiciones: no dice nada.
5.143 La contradicción es algo común entre las proposiciones que ninguna proposición tiene en común con otra. La tautología es aquello común a todas las proposiciones que no tienen nada en común entre sí.
La contradicción se oculta, por así decirlo, fuera de todas las proposiciones; la tautología, dentro.
La contradicción es el límite externo de las proposiciones. La tautología, su centro insustancial.
- 5.15 Si Vr es el número de los fundamentos de verdad de la proposición «r» y Vrs el número de aquellos fundamentos de verdad de la proposición «s» que son al mismo tiempo los fundamentos de verdad de «r», entonces llamamos a la relación Vrs: Vr la medida de la probabilidad que la proposición «r» da a la proposición «s».
5.151 Sea en un esquema semejante al del número 5.101, Vr el número de las «V» en la proposición r; Vrs el número de «V» en la proposición s que se encuentra en la misma columna que «V» de la proposición r.
Entonces la proposición r da a la proposición s la probabilidad Vrs: Vr.
- 5.1511 No hay ningún objeto especial que sea propio de las proposiciones-probabilidades.
5.152 A las proposiciones que no tienen ningún argumento de verdad en común las llamamos independientes entre sí.
Dos proposiciones elementales dan recíprocamente la probabilidad 1/2.
Si p se sigue de q, la proposición «q» da a la proposición «p» la probabilidad 1. La certeza de la conclusión lógica es un caso límite de la probabilidad.
(Aplicación a la tautología y contradicción.)
- 5.153 Una proposición no es en sí misma ni probable ni improbable. Un acontecimiento ocurre o no ocurre; no hay término medio.
5.154 En una urna hay el mismo número de bolas blancas y negras (y no otras). Yo extraigo una bola después de otra y las vuelvo a poner en la urna. Así puedo determinar, por un experimento, que el número de las bolas negras y el de las blancas extraídas tiende a aproximarse según prosigue la extracción.
Esto no es ningún hecho matemático. Ahora, si yo digo: Es igualmente probable que extraiga una bola negra que una blanca, esto significa que todas las circunstancias que me son conocidas (incluyendo las leyes de la naturaleza hipotéticamente admitidas) no me dan más la probabilidad de que ocurra un acontecimiento que la de que ocurra otro. Se da, pues –como se puede fácilmente comprender por la explicación anterior-, para cada posible acontecimiento la probabilidad 1/2.
Lo que yo verifico por el experimento es que el que ocurran los dos acontecimientos es independiente de las circunstancias que no me son conocidas como más próximas.
- 5.155 La unidad de la proposición-probabilidad es: las circunstancias –las cuales yo no conozco con la suficiente amplitud- dan al ocurrir de un acontecimiento determinado tal y tal grado de probabilidad.
5.156 Probabilidad es una generalización.
Esto implica una descripción general de una forma proposicional.
Sólo en defecto de la certeza utilizamos la probabilidad. Aun cuando no conozcamos perfectamente un hecho, sabemos, sin embargo, algo sobre su forma.
(Una proposición puede ser una figura incompleta de un cierto estado de cosas, pero es siempre una figura completa.)
La proposición-probabilidad es algo semejante a un extracto de otras proposiciones.
- 5.2 Las estructuras de las proposiciones están unas respecto de otras en relaciones internas.
- 5.21 Nosotros podemos poner de relieve estas internas relaciones en nuestros modos de expresión, presentando una proposición como el Resultado de una operación que la obtiene de otras proposiciones (las bases de la operación).
- 5.22 La operación es la expresión de una relación entre las estructuras de su resultado y sus bases.
- 5.23 La operación es aquello que hay que hacer con una proposición para obtener otra de ella.
- 5.231 Y esto depende, naturalmente, de sus propiedades formales, de la interna semejanza de sus formas.
- 5.232 La relación interna que ordena una serie es equivalente a la operación por la cual un término procede de otro.
- 5.233 La operación puede tener lugar primeramente cuando una proposición procede de otra de un modo lógicamente significante. Es decir, cuando comienza la construcción lógica de la proposición.
- 5.234 Las funciones de verdad de la proposición elemental son resultados de operaciones que tienen por base las proposiciones elementales. (Llamo a estas operaciones, operaciones de verdad)
5.2341 El sentido de una función de verdad de p es una función del sentido de p.
Negación, adición lógica, multiplicación lógica, etc., etc., son operaciones. (La negación invierte el sentido de una proposición.)
5.24 La operación se muestra en una variable; muestra cómo podemos pasar de una forma de proposición a otra.
La operación da expresión a las diferencias de las formas. (Y aquello que hay de común entre las bases y el resultado de la operación son propiamente las bases.)
- 5.241 La operación no caracteriza ninguna forma sino sólo las diferencias de las formas.
- 5.242 La misma operación que obtiene «q» de «p» obtiene «r» de «q» y así sucesivamente. Esto sólo puede expresarse por el hecho de que «p», «q», «r», etc., son variables que expresan de modo general ciertas relaciones formales.
5.25 El que ocurra una operación no caracteriza el sentido de una proposición.
La operación no dice nada; sólo dice su resultado, y esto depende de las bases de la operación.
(No deben confundirse operación y función.)
- 5.251 Una función no puede ser su propio argumento, pero el resultado de una operación puede ser su propia base.
- 5.252 Sólo por este procedimiento es posible el progreso de un término a otro término en una serie formal (de tipo a tipo en la jerarquía de Russell y de Whitehead). (Russell y Whitehead no han admitido la posibilidad de este progreso, pero han hecho uso de él continuamente.)
5.2521 A la aplicación repetida de una operación a su propio resultado le llamo su sucesiva aplicación («O’ O’ O’ a» es el resultado de la triple aplicación sucesiva de «O’ξ» a «a»).
En un sentido semejante hablo yo de la aplicación sucesiva de múltiples operaciones a un número de proposiciones.
- 5.2522 El término general de la serie formal a, O’ a, O’ O’ a,. . . lo escribo, pues, así: «[a, x, O’ x]». Esta expresión entre paréntesis es una variable. El primer término de la expresión es el comienzo de la serie formal; el segundo, la forma de un término cualquiera de la serie, y el tercero, la forma de aquel término de la serie que sigue inmediatamente a x.
- 5.2523 El concepto de la aplicación sucesiva de una operación es equivalente al concepto de «y así sucesivamente».
- 5.253 Una operación puede invertir el efecto de otra. Las operaciones pueden anularse unas a las otras.
- 5.254 Las operaciones pueden desaparecer (por ejemplo, la negación en «~ ~p». ~ ~ p=p).
5.3 Todas las proposiciones son el resultado de operaciones de verdad con proposiciones elementales.
La operación de verdad es el modo y manera de que resulte de las proposiciones elementales la función de verdad.
De acuerdo con la naturaleza de las operaciones de verdad, del mismo modo que de las proposiciones elementales nace su función de verdad, de las funciones de verdad nace una nueva. Cada operación de verdad crea de las funciones de verdad de las proposiciones elementales otra función de verdad de proposiciones elementales, es decir, una proposición. El resultado de cada operación de verdad sobre el resultado de las operaciones de verdad sobre las proposiciones elementales es también el resultado de una operación de verdad sobre las proposiciones elementales.
Toda proposición es el resultado de operaciones de verdad sobre proposiciones elementales.
- 5.31 El esquema núm. 4.31 tiene también un significado si «p», «q», «r», etc., no son proposiciones elementales. Y es fácil ver que el signo proposicional en el núm. 4.42 expresa una función de verdad de las proposiciones elementales, aun que «p», «q» sean funciones de verdad de las proposiciones elementales.
- 5.32 Todas las funciones de verdad son resultado de la sucesiva aplicación de un número finito de operaciones de verdad a proposiciones elementales.
- 5.4 Aparece, pues, claro que no hay «objetos lógicos», «constantes lógicas» (en el sentido de Frege y de Russell).
- 5.41 Así, pues, todos aquellos resultados de operaciones de verdad sobre funciones de verdad, que son una y la misma función de verdad de las proposiciones elementales, son idénticos.
5.42 Es evidente que v, ɔ, etc., no son relaciones en el sentido de derecha e izquierda, etc.
La posibilidad de una definición en cruz de los «signos primitivos» lógicos de Frege y Russell, muestra por si misma que no son signos primitivos y que no designan relaciones.
Y es claro que el «ɔ» que definíamos mediante «~» y «v» es idéntico a aquel con el cual definíamos «v» mediante «~», y que este «v» es idéntico con el primero, y así sucesivamente.
5.43 Que de un hecho p deban seguirse infinitos otros, a saber: ~ ~p, ~ ~ ~ ~p, etc., cuesta mucho creerlo, y no menos sorprendente es que el infinito número de proposiciones de la lógica (de la matemática) derive de media docena de «proposiciones primitivas».
Todas las proposiciones de la lógica dicen lo mismo. Es decir, nada.
5.44 Las funciones de verdad no son funciones materiales.
Si, por ejemplo, una afirmación puede producirse por negaciones repetidas, ¿está la negación –en cierto sentido contenida en la afirmación? ¿niega «~ ~p» ~p o afirma p; o una y otra cosa?
La proposición «~ ~p» -no trata de la negación como de un objeto, sino que la posibilidad de la negación está ya prejuzgada en la afirmación.
Y si existiese un objeto llamado «~», entonces «~ ~p» debería decir algo distinto a «p». Pues una proposición trataría de ~, la otra no.
- 5.441 Esta desaparición de las constantes lógicas aparentes también ocurre si « ~(∃x) . ~fx» dice lo mismo que «(x) . fx», o «(∃x) . fx . x=a» lo mismo que «fa».
- 5.442 Dada una proposición, con ella están ya dados los resultados de todas las operaciones de verdad que tiene de base.
- 5.45 Si hay signos primitivos lógicos, una lógica correcta debe aclarar sus posiciones respectivas y justificar su existencia. La construcción de la lógica desde sus signos primitivos, debe ser clara.
5.451 Si la lógica tiene ideas primitivas, éstas deben ser independientes unas de otras. Si se introduce una idea primitiva, debe introducirse en todo el contexto en el cual se encuentra. No se puede, pues, introducirla primero para un contexto, después para otro. Por ejemplo: Si se introduce la negación debemos entenderla tanto en las proposiciones de la forma « ~p» como en las proposiciones «~(pvq)», «(∃x).~fx» y otras. No podemos introducirla primero para una clase de casos y después para otra, pues permanecería dudoso cuando su significado fuese el mismo en los dos casos, y no habría ninguna razón para usar el mismo modo de simbolización en ambos.
(En resumen, que lo que Frege (Grundgesetze der Arithmetik) ha dicho acerca de la introducción de los signos mediante definiciones, vale, mutatis mutandis, para la introducción de los signos primitivos.)
5.452 La introducción de un nuevo expediente en el simbolismo de la lógica debe ser siempre un acontecimiento pleno de consecuencias. No se puede introducir en lógica ningún nuevo expediente entre paréntesis o al margen que tenga, por así decirlo, un aire absolutamente inocente.
(Así, en los Principia Mathematica de Russell y Whitehead se encuentran definiciones y proposiciones primitivas en palabras. ¿Por qué aquí palabras de repente? Esto necesitaría una justificación. Esta falta, y tiene que faltar porque el procedimiento es de hecho ilícito.)
Pero si se ha demostrado la necesidad de introducir un nuevo expediente en un lugar, debemos sin más preguntarnos:
¿Dónde debe usarse siempre este expediente? Su posición en lógica debe aclararse.
5.453 En lógica todos los números deben ser susceptibles de justificación.
O mejor; debe resultar esto: que en lógica no hay números.
No hay números privilegiados.
5.454 En lógica no hay un estar uno al lado del otro, no puede darse ninguna clasificación.
En lógica no puede darse un más general y un más especial.
5.4541 Las soluciones de los problemas lógicos deben ser sencillas, pues ellas establecen los tipos de la simplicidad.
Los hombres han tenido siempre la vaga idea de que debía haber una esfera de cuestiones cuyas respuestas -a priori- estuviesen simétricamente unidas en una estructura acabada y regular.
Una esfera en la cual sea válida la proposición: simplex sigillum veri.
- 5.46 Sí se introduce correctamente los signos lógicos, se introduce también con ellos el sentido de todas sus combinaciones; no sólo «pvq», sino también «~(pv~q)», etc., etc. Con esto se habría introducido también el efecto de todas las posibles combinaciones de paréntesis. Y así se pondría en claro que los signos primitivos generales propiamente dichos no son «pvq» «(qx).∃x)», etc., etc., sino la forma más general de sus combinaciones.
5.461 Es muy significativo el hecho, en apariencia sin importancia, de que las pseudo-relaciones lógicas como v y e - contrariamente a las relaciones reales- tengan necesidad de paréntesis.
El uso de paréntesis con estos signos, aparentemente primitivos, indica que no son verdaderos signos primitivos; y, desde luego, nadie creerá que los paréntesis tienen un significado por sí mismos.
- 5.4611 Los signos de las operaciones lógicas son interpunciones.
5.47 Es claro que todo lo que se pueda decir de antemano sobre la forma de todas las proposiciones, se puede decir de una sola vez.
Pues todas las operaciones lógicas están ya contenidas en las proposiciones elementales. Pues «fa» dice lo mismo que
«(∃x).fx.x=a».
Dónde hay composición hay argumento y función, y donde ellos están, ya están todas las constantes lógicas.
Se podría decir: La única constante lógica es aquello que todas las proposiciones tienen en común unas con otras según su naturaleza.
Pero ésta es la forma general de la proposición.
- 5.471 La forma general de la proposición es la esencia de la proposición.
- 5.4711 Dar la esencia de la proposición significa dar la esencia de toda descripción; o sea, la esencia del mundo.
- 5.472 La descripción de la forma más general de la proposición es la descripción del único y propio signo primitivo general de la lógica.
5.473 La lógica debe bastarse a sí misma.
Un signo posible debe también poder designar. Todo lo que en lógica es posible, está también permitido. («Sócrates es idéntico» no quiere decir nada, porque no hay ninguna propiedad que se llame
«idéntico». Tal proposición no tiene sentido porque no habíamos establecido ninguna de terminación arbitraria, pero no porque el símbolo sea en y por sí mismo ilícito.)
En cierto sentido, en lógica no podemos equivocarnos.
- 5.4731 La evidencia, de la cual Russell tanto habla, sólo podría descartarse en lógica si el lenguaje mismo impidiese todo error lógico. –Que la lógica sea un a priori consiste en esto, en que no se puede pensar ilógicamente.
- 5.4732 No podemos dar a un signo un sentido falso.
- 5.47321 El principio de Ockam no es naturalmente una regla arbitraria ni tampoco una regla justificada por su éxito práctico: dice simplemente que todos los elementos innecesarios en un simbolismo no significan nada. Los signos que cumplen un fin son lógicamente equivalentes; los signos que no cumplen ningún fin carecen lógicamente de significado.
- 5.4733 Frege dice: Toda proposición legítimamente construida debe tener un sentido: y yo digo: Toda proposición posible está legítimamente construida, y si no tiene sentido esto se debe únicamente a que no le hemos dado un significado a cualquiera de sus partes constitutivas.
- 5.474 El número de las operaciones necesarias depende solo de nuestra notación.
- 5.475 Es sólo cuestión de construir un sistema de signos con un número determinado de dimensiones – con una determinada multiplicidad matemática.
- 5.476 Es claro que no se trata aquí de un número de ideas primitivas que deben ser designadas, sino de la expresión de una regla.
5.5 Cada función de verdad es un resultado de la sucesiva aplicación de la operación (-----V) (ξ,... ) a las proposiciones elementales.
Esta operación niega todas las proposiciones del paréntesis de la derecha y la llamo la negación de estas proposiciones.
- 5.50
5.501 Una expresión entre paréntesis cuyos términos son proposiciones la indico –si el orden de los términos entre paréntesis es indiferente- con un signo de la forma «(-ξ)». «ξ» es una variable cuyos valores son los términos de la expresión entre paréntesis, y la línea sobre la variable indica que ésta representa todos su valores en el paréntesis.
(Así, pues, si ξ tiene tres valores P, Q, R; entonces (-ξ)=(P, Q, R))
Los valores de la variable deben determinarse.
La determinación es la descripción de las proposiciones representadas en la variable.
El modo cómo se haga la descripción de los términos de la expresión entre paréntesis no es esencial.
Podemos distinguir tres clases de descripción: 1. La enumeración directa. En este caso podemos poner, simplemente, en lugar de la variable sus valores constantes. 2. La indicación de una función fx, cuyos valores para todos los valores de x son las proposiciones a describir. 3. La indicación de una ley formal de acuerdo con la cual se construyen tales proposiciones. En este caso los términos de la expresión entre paréntesis son todos los términos de una serie formal.
- 5.502 En vez de «(- - - - - V) (ξ, . . . .)» escribo, por consiguiente, «N(-ξ)». N(-ξ) es la negación de todos los valores de la variable proposicional ξ.
- 5.503 Puesto que es obvio que es fácilmente expresable cómo se pueden construir proposiciones con esta operación y cómo no se deben construir me diante ella, esto tiene también que hallar una expresión exacta.
- 5.51 Si ξ tiene sólo un valor, entonces N(-ξ)=~p (no p). Si tiene dos valores, entonces, (N-ξ)= ~p.~q (ni p ni q).
- 5.511 ¿Cómo es posible que la lógica, que todo lo abarca y que refleja el mundo, use de tan especiales garabatos y manipulaciones? Sólo porque todas están unidas por una trama infinitamente fina al gran espejo.
5.512 «~p» es verdadera si «p» es falsa. Así, pues, en la proposición verdadera «~p», «p» es una proposición falsa. ¿Cómo es posible que el rasgo «~» la ponga de acuerdo con la realidad?
Aquello que niega en «~p» no es, sin embargo, «~», sino aquello que todos los signos de esta notación, que niegan a p, tienen en común.
De aquí la regla común «~p», «~~~p», «~pv~p», «~p.~p», etc., etc., según la cual se construyen (ad infinitum). Y esto, que es común, refleja la negación.
5.513 Se podría decir: Lo que es común a todos los símbolos que aseveran tanto p como q, es la pro posición «p . q». Lo que es común a todos los símbolos que aseveran p o q es la proposición «pvq».
Y de modo semejante podríamos decir: Dos proposiciones se oponen la una a la otra cuando no tienen nada en común. Y cada proposición tiene sólo una negativa, porque sólo hay una proposición que se encuentre totalmente fuera de ella.
Así, también en la notación de Russell aparece que «q : pv. ~p» dice lo mismo que «q» ; «pv ~p» no dice nada.
- 5.514 Si una notación está fijada, se da con ella una regla según la cual se construyen todas las proposiciones que niegan p; una regla según la cual se construyen todas las proposiciones que aseveran p; una regla según la cual se construyen todas las proposiciones que aseveran p o q y así sucesivamente. Estas reglas son equivalentes a los símbolos, y en ellas se refleja su sentido.
5.515 De nuestros símbolos aparece que lo que está recíprocamente unido por «v», «.», etc., deben ser proposiciones.
Y éste es el caso, pues los símbolos «p» y «q» presuponen «v», «~», etc. Si el signo «p» en «pvq» no está por un signo complejo, no puede tener sentido por sí solo; pero entonces los signos «pvp», «p . p», etc., que tienen el mismo sentido que «p», no tienen sentido. Pero si «pvp» no tiene sentido, tampoco puede tenerlo «pvq».
5.5151 ¿Debe el signo de la proposición negativa construirse con el signo de la positiva? ¿Por qué no se podría expresar la proposición negativa por medio de un hecho negativo? (Por ejemplo: Si «a» no está en una cierta relación con «b», esto podría expresar que «aRb» no acaece.)
Pero también aquí la proposición negativa está indirectamente construida mediante la positiva.
La proposición positiva debe presuponer la existencia de la proposición negativa y viceversa.
- 5.52 Si los valores de ξ son todos los valores de una función fx, para todos los valores de x entonces N(-ξ) = ~(∃x) . fx.
5.521 Yo separo el concepto todo de la función de verdad.
Frege y Russell han introducido la generalidad en conexión con el producto lógico o la suma lógica. Se hace así difícil entender la proposición «(∃x) . fx» y «(x) . fx», en la cual las dos ideas quedan encerradas.
- 5.522 La peculiaridad del signo de generalidad es, en primer lugar, que refiere a un prototipo lógico, y en segundo lugar que pone de relieve las constantes.
- 5.523 El signo de generalidad interviene como un argumento.
5.524 Si los objetos están dados, con ellos están dados también todos los objetos.
Si las proposiciones elementales están dadas, están dadas con ellas todas las proposiciones elementales.
5.525 No es correcto traducir la proposición «(∃x) . fx» -como Russell hace- en palabras, poniendo «fx es posible».
Certeza, posibilidad o imposibilidad de un estado de cosas no se expresan por una proposición, sino porque una expresión es una tautología, una proposición con significado o una contradicción.
Aquel precedente al cual siempre se puede apelar debe ya estar en el símbolo mismo.
5.526 Se puede describir plenamente el mundo por proposiciones completamente generalizadas; es decir, sin coordinar de antemano un nombre a un objeto determinado.
Así, pues, para llegar al modo habitual de expresarse se necesita simplemente después de una expresión «hay una y solo una x, que... », decir: y esta x es a.
5.5261 Una proposición completamente generalizada es, como toda otra proposición, compuesta. (Esto se muestra en el hecho de que en «(∃x, Φ) . Φx» debemos mencionar «Φ» y «x» separadamente. Así están ambos en relación significativa con el mundo de modo independiente, como ocurre en la proposición no generalizada.)
Característica del símbolo compuesto: tiene algo en común con otros símbolos.
5.5262 La verdad o falsedad de cada proposición altera algo en la estructura general del mundo. Y el campo que se deja a esta estructura por la totalidad de las proposiciones elementales es exactamente aquel que delimitan las proposiciones completamente generales.
(Si una proposición elemental es verdadera, entonces, en todo caso, una proposición elemental más es verdadera.)
- 5.53 Expreso la identidad del objeto por la identidad del signo y no por medio de un signo de identidad. Y la diversidad de los objetos por la diversidad de los signos.
- 5.530
5.5301 Que la identidad no es una relación entre objetos es obvio. Esto se esclarece, por ejemplo, completamente si consideramos la proposición «(x): fx . ɔ . x=a». Lo que esta proposición dice es simplemente que sólo a satisface la función f, y no que sólo aquellas cosas que tienen una cierta relación con a satisfagan la función f.
Se podría naturalmente decir que en efecto solamente a tiene esta relación respecto de a, pero para expresar esto necesitaríamos del propio signo de identidad.
5.5302 La definición de Russell de «=» no basta; porque, según ella, no se puede decir que dos objetos tengan todas sus propiedades en común. (Incluso si esta preposición no es nunca verdadera, tiene, sin embargo, sentido.)
- 5.5303 Sea dicho de paso: decir de dos cosas que son idénticas es un sin sentido, y decir de una que es idéntica consigo misma no es decir nada.
- 5.531 Yo no escribo, pues, «f(a, b) . a = b», sino «f(a, a)» (o «f(b, b)»). Y no «f(a, b). ~a=b», sino «f(a, b)».
5.532 Y análogamente: no «(∃x, y) . f(x, y) , f(x, y)» sino «(∃x) . f(x, x)»; y no «(∃x, y) . f(x, y) . ~x=y», sino «(∃x, y) . f(x, y)».
(Y así en lugar del russelliano «(∃x, y) . f(x, y)»: «(∃x, y) . f(x . y) . v . (∃x) . f(x, x)».)
- 5.5321 En lugar de «(x) : fx ɔ x=a» escribimos, pues, por ejemplo, «(∃x) . fx . ɔ . fa ~(∃x, y) . fx.fy)». Y la proposición «sólo una x satisface f ( )», se lee: «(∃x) . fx : ~(∃x, y) . fx . fy».
- 5.533 El signo de identidad no es, pues, una parte esencial del simbolismo lógico.
- 5.534 Vemos ahora que pseudo-proposiciones como: «a=a», a=b . b=c . ɔ a=c», «(x) . x=x», «(∃x) . x=a», etc., no se pueden escribir por completo en un simbolismo lógico correcto.
5.535 De este modo desaparecen todos aquellos problemas que estaban en conexión con tales pseudoproposiciones.
Aquí están resueltos todos los problemas que lleva consigo el «Axiom of Infinity» de Russell.
Lo que el axioma del infinito quiere decir, se expresaría en el lenguaje por el hecho de que hay un infinito número de nombres con diferentes significados.
5.5351 Hay ciertos casos en los que uno está tentado de utilizar expresiones de la forma «a=a» o «p ɔ p». Así ocurre, por ejemplo, cuando se habla del arquetipo: proposición, cosa, etc. Russell, en los Principles of Mathematics, ha traducido en símbolos el sinsentido «p es una proposición» por «p ɔ p» y lo ha puesto como hipótesis delante de ciertas proposiciones para mostrar que sus lugares de argumento sólo podrían ocuparlos proposiciones.
(Es ya un sin sentido colocar la hipótesis «p ɔ p» delante de una proposición para asegurarle argumentos de la forma correcta, porque la hipótesis, cuando tiene como argumento una no-proposición, no se hace falsa, sino sin sentido, y porque la propia proposición se hace un sinsentido si tiene argumentos de especie equivocada; por consiguiente, no protege ni mejor ni peor del argumento erróneo que la hipótesis sin sentido añadida con este fin.)
- 5.5352 Igualmente si se quiere expresar «no hay cosas» por «~(∃x) . x=x ». Pero incluso si esto fuese una proposición, ¿no sería verdadera si, en efecto, «hubiese cosas», pero que no fuesen idénticas consigo mismas?
- 5.54 En la forma proposicional general la proposición entra en otra sólo como base de las operaciones de verdad.
5.541 A primera vista parece que una proposición podría entrar en otra de diferente modo.
Especialmente en ciertas formas proposicionales de la psicología, como «A cree que p acaecerá» o «A piensa p», etc.
A una consideración superficial puede parecer que la proposición p está en una cierta relación con el objeto A.
(Y en la moderna teoría del conocimiento (Russell, Moore, etc.), estas proposiciones se han concebido de este modo.)
- 5.542 Pero es claro que «A cree que p», «A piensa p», «A dice p», son de la forma «‘p’ dice p»; y aquí se trata no de la coordinación de un hecho y un objeto, sino de la coordinación de hechos por la coordinación de sus objetos.
5.5421 Esto muestra que el alma –el sujeto, etc.-, como se le concibe en la superficial psicología de hoy, es un absurdo.
Un alma compuesta no sería más un alma.
- 5.5422 La explicación correcta de la forma de la proposición «A juzga p» debe mostrar que es imposible juzgar un sinsentido. (La teoría de Russell no satisface esta condición.)
5.5423 Percibir un complejo quiere decir percibir que sus partes constitutivas están combinadas entre sí de tal y tal modo.
Esto quizás explique que la figura
pueda verse de dos modos como un cubo; y todos los demás fenómenos similares. Pues, en realidad, nosotros vemos dos hechos diferentes.
(Si yo me fijo primero en el ángulo a y sólo de pasada en el b, a parece delante y b detrás, y viceversa.)
5.55 Debemos ahora responder a priori a la cuestión de todas las posibles formas de las proposiciones elementales.
La proposición elemental consta de nombres, pero así como no podemos dar el número de los nombres con diferente significado, tampoco podemos dar la composición de las proposiciones elementales.
5.551 Nuestro principio fundamental es que toda cuestión que pueda revolverse por, la lógica, puede resolverse sin más.
(Y si llegásemos a una situación en que tuviésemos necesidad de contemplar el mundo para poder responder a un tal problema, esto sería señal de que seguíamos un camino fundamentalmente equivocado).
5.552 La «experiencia», de la que, tenemos necesidad para entender la lógica, no es que algo ocurra de tal y tal modo, sino que algo es; pero esto no es experiencia.
La lógica precede a toda experiencia –que algo es así. Es antes que el cómo, no que el qué.
- 5.5521 Y si no fuese así, ¿cómo podríamos aplicar la lógica? Se podría decir: Si hubiese una lógica, aunque no hubiese un mundo, ¿cómo podría haber una lógica puesto que hay un mundo?
- 5.553 Russell dice que hay relaciones simples entre diferentes números de cosas (individuos). Pero ¿entre qué números? Y ¿cómo se decidiría ésto? ¿Por la experiencia? (No hay números privilegiados.)
- 5.554 La indicación de cualquier forma especial sería enteramente arbitraria.
- 5.5541 Se debe poder determinar a priori, por ejemplo, si yo podría encontrarme en la necesidad de designar algo con el signo de una relación de 27 términos.
5.5542 Pero ¿podríamos hacernos semejante pregunta? ¿Podríamos establecer una forma de signo sin saber si podría corresponderle algo?
¿Tiene sentido la pregunta: Qué debe ser, para que algo acaezca?
5.555 Es claro que nosotros tenemos un concepto de la proposición elemental, prescindiendo de su especial forma lógica.
Pero donde se puedan construir símbolos según un sistema, es este sistema lo lógicamente importante, y no los símbolos particulares.
Y como puede ser posible que yo haya de ocuparme en lógica de formas que puedo inventar, yo debo, pues, ocuparme de aquello que me permite inventarlas.
- 5.556 No puede haber una jerarquía de las formas de las proposiciones elementales. Sólo aquello que nosotros mismos construimos puede preverse.
5.5561 La realidad empírica está limitada por la totalidad de los objetos. El límite aparece de nuevo en la totalidad de las proposiciones elementales.
Las jerarquías son y deben ser independientes de la realidad.
- 5.5562 Si por razones puramente lógicas nosotros sabemos que debe haber proposiciones elementales, entonces esto debe saberlo cualquiera que entienda las proposiciones en su forma no analizada.
5.5563 Todas las proposiciones de nuestro lenguaje corriente están efectivamente, tal y como son, ordenadas de un modo completamente lógico. La cosa más simple que nosotros debemos indicar aquí no es una imagen de la verdad, sino la propia vendad completa.
(Nuestros problemas no son abstractos, sino quizá los más concretos que hay).
5.557 La aplicación de la lógica decide qué proposiciones elementales hay.
La lógica no puede anticiparse a aquello que se encuentra en su aplicación.
Esto es claro: la lógica no puede entrar en conflicto con su aplicación.
Pero la lógica debe estar en contacto con su aplicación.
La lógica y su aplicación no deben sobreponerse una a la otra.
- 5.5571 Si yo no puedo indicar las proposiciones elementales a priori, querer indicarlas debe llevar a un obvio sinsentido.
- 5.6 Los límites de mi lenguaje significan los límites de mi mundo.
5.61 La lógica llena el mundo; los límites del mundo son también sus límites.
Nosotros no podemos, pues, decir en lógica: en el mundo hay esto y lo de más allá; aquello y lo otro, no.
Esto parece, aparentemente, presuponer que excluimos ciertas posibilidades, lo que no puede ser, pues, de lo contrario, la lógica saldría de los límites del mundo; esto es, siempre que pudiese considerar igualmente estos límites también desde el otro lado.
Lo que no podemos pensar no podemos pensarlo. Tampoco, pues, podemos decir lo que no podemos pensar.
5.62 Esta observación da la clave para decidir acerca de la cuestión de cuanto haya de verdad en el solipsismo.
En realidad, lo que el solipsismo significa es totalmente. correcto; sólo que no puede decirse, sino mostrarse.
Que el mundo es mi mundo, se muestra en que los límites del lenguaje (el lenguaje que yo sólo entiendo) significan los límites de mi mundo.
- 5.621 Mundo y vida son una sola cosa.
- 5.63 Yo soy mi mundo. (El microcosmos).
5.633 ¿Dónde en el mundo puede observarse un sujeto metafísico? Tú dices que aquí ocurre exactamente como con el ojo y el campo de visión; pero tú no ves realmente el ojo.
Y nada en el campo de visión permite concluir que es visto por un ojo.
5.6331 El campo de visión no tiene ciertamente esta forma:
5.634 Esto está en conexión con el hecho de que ninguna parte de nuestra experiencia es a priori.
Todo lo que nosotros vemos podría ser de otro modo.
Todo lo que nosotros podemos describir Podría también ser de otro modo.
No hay ningún orden a priori de las cosas.
- 5.64 Vemos aquí cómo el solipsismo llevado estrictamente coincide con el puro realismo. El yo del solipsismo se reduce a un punto inextenso y que da la realidad coordinada con él.
5.641 Hay, pues, ciertamente un sentido en el cual se puede hablar en filosofía del yo de un modo no psicológico.
El yo entra en filosofía por el hecho de que «el mundo es mi mundo».
El yo filosófico no es el hombre, ni el cuerpo humano, ni tampoco el alma humana de la cual trata la psicología, sino el sujeto metafísico, el limite –no una parte del mundo.

6 La forma general de una función de verdad es: [p, -ξ N(-ξ)].
Esta es la forma general de la proposición.
- 6.0
- 6.00
- 6.001 Esto no dice otra cosa sino que toda proposición es el resultado de las sucesivas aplicaciones de la operación N’(-ξ) a las proposiciones elementales.
- 6.002 Dada la forma general según la cual se construye una proposición, se da con ella también la forma general según la cual se puede obtener de una proposición otra proposición por medio de una operación.
6.01 La forma general de la operación Ω’(-η) es, pues: [-ξ,N(-ξ) ]’ (-η)('='[,-ξ,N(-ξ)]).
Esta es la forma más general de transición de una proposición a otra.
6.02 Y así llegamos a los números. Yo defino:
x = Ω°, x Def. y
Ω’Ω supr(v), x= Ω supr(v+1), x Def.
Según estas reglas de signos, escribimos también la serie x, Ω’ x, Ω ‘ Ω’ x, Ω’ Ω’ Ω’ x,......
así: Ω°, x, Ω°+1, x, Ω°+1+1, x, Ω°+1+1+1, x,...
Yo escribo, pues, en lugar de «[ x, ξ, Ω’ ξ ]»: «[ Ω°, x, Ω supr(v), x, Ω supr(v+1), x]».
Y defino:
0+1=1 Def.
0+1+1=2 Def.
0+1+1+1=3 Def. (etc.)
- 6.021 El número es el exponente de una operación.
6.022 El concepto de número no es sino aquello que es común a todos los números, la forma general del número.
El concepto de número es el número variable.
Y el concepto de igualdad numérica es la forma general de todas las igualdades numéricas particulares.
- 6.03 La forma general del número entero es: [o, ξ, ξ+1].
6.031 La teoría de las clases es superflua en matemáticas.
Esto está en conexión con el hecho de que la generalidad de la cual tenemos necesidad en matemáticas, no es la accidental.
- 6.1 Las proposiciones de la lógica son tautologías.
- 6.11 Por consiguiente, las proposiciones de la lógica no dicen nada. (Son proposiciones analíticas.)
- 6.111 Las teorías que hacen que una proposición de la lógica aparezca plena de contenido, son siempre falsas. Se puede, por ejemplo, creer que las palabras «verdadero» y «falso» significan dos propiedades entre otras propiedades, y así aparecería como un hecho extraño que toda proposición: poseyese una de estas propiedades. Esto no parece ahora ya tan evidente, no más evidente que la proposición «todas las rosas son amarillas o rojas», aunque fuese verdadera. Así, pues, aquella proposición ha tomado el carácter de una proposición científica, y ésta es una señal segura de qué había sido falsamente entendida.
- 6.112 La correcta explicación de las propiedades lógicas debe darla una posición peculiar entre todas las otras proposiciones.
- 6.113 La señal característica de las proposiciones lógicas está en que se puede reconocer sólo en el símbolo que son verdaderas o falsas; y este hecho contiene en sí toda la filosofía de la lógica. Y es también uno de los hechos -más importantes que la verdad o la falsedad de las proposiciones no lógicas, no se pueda reconocer sólo en la proposición.
6.12 El hecho de que las proposiciones de la lógica sean tautológicas muestra las propiedades formales –lógicas- del lenguaje, del mundo.
Que sus partes constitutivas así unidas den una tautología caracteriza la lógica de sus partes constitutivas.
Para que las proposiciones unidas de modo y manera determinados den una tautología, han de tener determinadas propiedades de estructura.
Que así unidas den una tautología indica también que poseen estas propiedades de estructura.
- 6.120
- 6.1201 Que, por ejemplo, las proposiciones «p» y «~p» en la unión «~(p . ~p)» den una tautología, indica que se contradicen entre si. Que las proposiciones «p ɔ q», «p» y «q» unidas entre sí en la forma «(p ɔ q) . (p) : ɔ : (q)», den una tautología, indica que q procede de p y p ɔ q. Que «(x) . fx : ɔ : fa» sea una tautología indica que fa se sigue de (x) . fx, etc., etc.
- 6.1202 Es claro que pueden utilizarse con este fin las contradicciones en lugar de las tautologías.
6.1203 Para reconocer una tautología como tal en los casos en que no entra en la tautología el signo de generalidad, podemos usar el siguiente método intuitivo: Escribo «VpF», «VqF», «VrF», etc., en lugar de «p», «q», «r», etc. Expreso las combinaciones de verdad por medio de paréntesis. Por ejemplo:
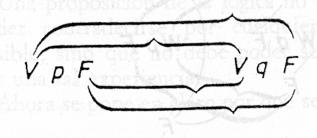
y la coordinación de la verdad o falsedad de toda la proposición con las combinaciones de verdad de los argumentos de verdad, por líneas, del modo siguiente:
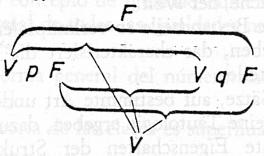
Este signo, por ejemplo, representaría la proposición p e q. Quiero ahora, por ejemplo, investigar si una proposición como ~(p . ~p) (principio de contradicción) es una tautología. La forma «~ξ» se escribe en nuestra notación
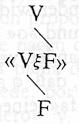
La forma «ξ . η» así:
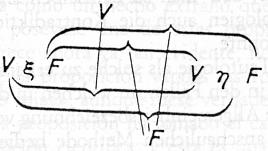
Por lo tanto, la proposición ~(p . ~q) resulta así:
Si ponemos «p» en lugar de «q» y examinamos la combinación más externa de las V y de las F con aquella más interna, resulta que la verdad de la proposición entera está coordinada con todas las combinaciones de verdad de sus argumentos; su falsedad con ninguna de las combinaciones de verdad.
6.121 Las proposiciones de la lógica demuestran las propiedades lógicas de las proposiciones que no dicen nada.
A este método se le podría llamar un método cero. En la proposición lógica, las proposiciones se ponen en equilibrio recíproco, y el estado de equilibrio indica cómo deben construirse lógicamente estas proposiciones.
- 6.122 De aquí resulta que podríamos también pasar sin las proposiciones lógicas, ya que en una notación correspondiente podríamos reconocer las propiedades formales de las proposiciones por una simple inspección.
6.1221 Si, por ejemplo, dos proposiciones, «p» y «q», dan una tautología en la conexión «p ɔ q», entonces es claro que q se sigue de p.
Que, por ejemplo, «q» se siga de «p ɔ q . p» lo vemos de estas dos mismas proposiciones; pero lo podíamos indicar también así: uniéndolas a «p ɔ q . p: ɔ q» y mostrando que esto es una tautología.
6.1222 Esto arroja luz sobre la cuestión de por qué las proposiciones lógicas no pueden ser confirmadas por la experiencia, lo mismo que contradecirlas la experiencia.
Una proposición de la lógica no sólo no debe poder contradecirse por cualquier experiencia posible, sino que no debe poder ser confirmada por una tal experiencia.
- 6.1223 Ahora se pone en claro por qué se siente a menudo que las «verdades lógicas» deben ser «postuladas» por nosotros: nosotros podemos, efectivamente, postularlas en cuanto podemos postular una adecuada notación.
- 6.1224 Y se pone también en claro por qué se ha llamado a la lógica la teoría de las formas y de la inferencia.
6.123 Es claro que las leyes de la lógica no pueden a su vez obedecer a las leyes de la lógica.
(No hay, como pensaba Russell, para cada «tipo» un principio particular de contradicción; uno basta, ya que no es aplicable a sí mismo.)
6.1231 La característica de las proposiciones lógicas no es su validez general.
Ser general significa, pues, solo valer de modo accidental para todas las cosas. Una proposición no generalizada puede ser tautológica tanto cuanto una generalizada.
- 6.1232 La validez lógica general podría llamarse esencial en contraposición a la accidental; por ejemplo: la de la proposición «todos los hombres son mortales». Proposiciones como el «Axioma de reducibilidad» de Russell no son proposiciones lógicas, y esto explica nuestro sentimiento de que aunque fuesen verdaderas sólo podrían serlo por una feliz casualidad.
- 6.1233 Se puede pensar un mundo en el cual el axioma de reducibilidad no sea válido. Pero es claro que la lógica no tiene nada que ver con la cuestión de si nuestro mundo es realmente así o no.
- 6.124 Las proposiciones lógicas describen la armazón del mundo o, mejor, la presentan. No «tratan» de nada, presuponen que los nombres tienen significado, y las proposiciones elementales, sentido; y ésta es su conexión con el mundo. Es claro que debe manifestar algo sobre el mundo el hecho de que resulten tautologías de uniones de símbolos, que tienen esencialmente un carácter determinado. Este es el punto decisivo. Decimos que en los símbolos que utilizamos algunas cosas son arbitrarias y otras no. La lógica expresa solamente esto último; pero esto significa que en lógica nosotros no expresamos por medio de los signos lo que queremos, sino que en lógica habla la naturaleza misma de los signos esencialmente necesarios. Si nosotros conocemos la sintaxis lógica de un lenguaje de signos cualquiera, entonces todas las proposiciones de la lógica están ya dadas.
- 6.125 Es posible también, según la vieja concepción de la lógica, dar de antemano una descripción de todas las «verdaderas» proposiciones lógicas.
- 6.1251 Por lo tanto, en lógica jamás puede haber sorpresas.
6.126 Es posible calcular si una proposición pertenece a la lógica calculando las propiedades lógicas del símbolo.
Y esto hacemos cuando «probamos» una proposición lógica. Pues sin preocuparnos del sentido y significado formamos la proposición lógica desde otras, según meras reglas simbólicas.
La prueba de una proposición lógica consiste en esto; en obtenerla de otras proposiciones lógicas por la aplicación sucesiva de ciertas operaciones con las cuales se continúa obteniendo de las primeras proposiciones nuevas tautologías. (Pues de una tautología solo tautologías se siguen.)
Naturalmente, este modo de manifestar que sus proposiciones son tautológicas, no es esencial a la lógica. Y es así por esta razón, porque las proposiciones de las cuales comienza la prueba deben indicar, sin pruebas, que son tautologías.
- 6.1261 En lógica, proceso y resultado son equivalentes. (No caben, pues, sorpresas.)
- 6.1262 La prueba en lógica es sólo un expediente mecánico para facilitar el reconocimiento de la tautología, cuando es complicada.
- 6.1263 Sería, sin duda, sorprendente que se pudiese probar lógicamente una proposición con significado por otra, y también una proposición lógica. Es claro de antemano que la prueba lógica de una proposición con significado y la prueba en lógica deben ser dos cosas por completo diferentes.
6.1264 La proposición con significado dice algo, y su prueba muestra que esto es así; en lógica toda proposición es la forma de una prueba.
Toda proposición de lógica es un modus ponens presentado en signos. (Y el modus ponens no puede ser expresado por una proposición.)
- 6.1265 La lógica se puede concebir siempre de tal modo que cada proposición sea su propia prueba.
6.127 Todas las proposiciones de la lógica tienen igual dignidad. No hay ningunas de ellas que sean proposiciones primitivas por esencia y otras derivadas.
Toda tautología muestra por sí misma que es una tautología.
- 6.1271 Es claro que el número de «proposiciones lógicas primitivas» es arbitrario, pues se puede deducir la lógica de una sola proposición primitiva, formando, por ejemplo, el producto lógico de las proposiciones primitivas de Frege. (Frege diría, quizá, que esta proposición primitiva no era del modo más inmediato evidente, pero es extraño que un pensador tan exacto como Frege tenga que recurrir al grado de evidencia como criterio de la proposición lógica.)
6.13 La lógica no es una doctrina, sino un reflejo del mundo.
La lógica es trascendental.
6.2 La matemática es un método lógico.
Las proposiciones de la matemática son ecuaciones, y, por consiguiente, pseudo-proposiciones.
- 6.21 Las proposiciones matemáticas no expresan ningún pensamiento.
6.211 No es, pues, nunca, en la vida, una proposición matemática lo que nosotros necesitamos, sino que utilizamos las proposiciones matemáticas sólo para inferir de proposiciones que no pertenecen a la matemática otras proposiciones, las cuales, igualmente, no pertenecen a las matemáticas.
(En filosofía, la cuestión «¿Con qué fin usamos propiamente tal palabra, tal proposición?», lleva siempre a resultados valiosos.)
- 6.22 La lógica del mundo, que en las proposiciones de la lógica aparece en tautologías, aparece en matemáticas en ecuaciones.
6.23 Si dos expresiones están unidas por el signo de igualdad, esto significa que puede sustituirse la una por la otra. Pero si éste es el caso, ambas expresiones deben mostrarlo por sí mismas.
Es característico de la forma lógica de dos expresiones que sean recíprocamente sustituibles.
6.231 Es una propiedad de la afirmación que se la pueda concebir como una negación doble.
Es una propiedad de «1 + 1 + 1 + 1», que pueda ser concebido como «(1 + 1) + (1 + 1)».
6.232 Frege dice que las dos expresiones tienen el mismo significado, pero distinto sentido.
Pero lo esencial en la ecuación consiste en que no es necesaria para indicar que ambas expresiones, que están unidas por el signo de igualdad, tienen el mismo significado: pues esto puede percibirse de las dos expresiones por sí mismas.
- 6.2321 Y que las proposiciones de las matemáticas puedan probarse, no significa otra cosa que su exactitud es reconocible sin necesidad de comparar, con los hechos, en cuanto a su exactitud, lo que ellas expresan.
- 6.2322 La identidad del significado de dos expresiones no puede ser aseverada. Pues para poder afirmar algo sobre su significado debo conocer su significado, y silo conozco, entonces sé si significan la misma o distinta cosa.
- 6.2323 La ecuación caracteriza sólo el punto de vista desde el cual considero las dos expresiones, es decir, el punto de vista de su igualdad de significado.
- 6.233 A la cuestión de si tenemos necesidad de la intuición para resolver los problemas matemáticos, se debe responder que en este caso el lenguaje mismo ofrece la intuición necesaria.
6.2331 El proceso del cálculo proporciona precisamente esta intuición.
El cálculo no es un experimento.
- 6.234 La matemática es un método de la lógica.
- 6.2341 Lo esencial del método matemático consiste en trabajar con ecuaciones. De este método depende, en efecto, que toda proposición matemática pueda entenderse por sí misma.
6.24 El método por el cual la matemática obtiene sus ecuaciones es el método de sustitución.
Pues las ecuaciones expresan la sustituibilidad de dos expresiones, y nosotros procedemos de un número dado de ecuaciones a otras nuevas ecuaciones, sustituyendo las expresiones por otras, de acuerdo con las ecuaciones.
6.241 Así, la prueba de la proposición 2 X 2 = 4 es la siguiente:
(Ωv)μ’ x= Ω v x μ’ x Def.
Ω supr(2x2) x=(Ω supr(2))supr(2)’ x=(Ω supr(2)) supr(1+1)’ x= Ω supr(2)’ Ω supr(2)’ x= Ω supr(1+1)’ Ω supr(1+1)’ x=(Ω’Ω)’(Ω’Ω)’ x= Ω’ Ω’ Ω’ Ω’ x= Ω supr(1+1+1+1)’ x=Ω supr(4)’x.
- 6.3 La investigación lógica significa la investiga ción de toda regularidad. Y fuera de la lógica todo es casual.
- 6.31 La llamada ley de inducción no puede en ningún caso ser una ley lógica, pues es, visiblemente, una proposición con significado. Por consiguiente, no puede ser una ley a priori.
- 6.32 La ley de causalidad no es una ley, sino la forma de una ley.
- 6.321 La «ley de causalidad» es un nombre de clase, y lo mismo que en mecánica hay, por ejemplo, las leyes del mínimum –tales como la ley de la acción mínima -, así, en física, hay leyes de causalidad, leyes de la forma de causalidad.
- 6.3211 Los hombres tienen de hecho la idea de que debe haber una «ley de la mínima acción», incluso antes de saber exactamente cómo sería. (Aquí como siempre, aquello que es cierto a priori resulta algo puramente lógico.)
- 6.33 Nosotros no creemos a priori en una ley de conservación, pero conocemos a priori la posibilidad de una forma lógica.
- 6.34 Todas las proposiciones tales como el principio de razón, la ley de la continuidad de la naturaleza, del mínimo de gasto en la naturaleza, etcétera, etc., todas son intuiciones a priori acerca de las posibles formas que se podrían dar a las proposiciones de la ciencia.
6.341 La mecánica newtoniana, por ejemplo, reduce la descripción del universo a una forma unitaria. Imaginémonos una superficie blanca con manchas negras irregulares. Digamos: Cualquier clase de figura que resulte puedo siempre aproximarla, tanto cuanto quiera, a su descripción si cubro la superficie con una malla reticular suficientemente fina, diciendo de cada cuadrícula que es blanca o negra. Habré reducido así la descripción de la superficie a una forma unitaria. Esta forma es arbitraria, pues yo hubiese podido aplicar con igual éxito una malla con aberturas triangulares o hexagonales. Pudiera ocurrir que la descripción hecha con una malla triangular fuese más sencilla; esto quiere decir que con una malla triangular más gruesa podríamos describir la superficie más exactamente que con una cuadrangular más fina, o al revés, y así sucesivamente.
A las diferentes mallas corresponden diversos sistemas de descripción del universo. La mecánica determina una forma de descripción diciendo: todas las proposiciones de la descripción del mundo deben obtenerse de un modo dado por un número dado de proposiciones –los axiomas de la mecánica-. Proporciona los ladrillos para construir el edificio de la ciencia y dice: cualquier edificio que tú quisieras levantar lo debes construir siempre con estos y solo con estos ladrillos.
(Lo mismo que con el sistema de los números se debe ser capaz de escribir arbitrariamente cualquier número, así con el sistema de la mecánica se debe poder escribir arbitrariamente cualquier proposición de la física.)
6.342 Ahora vemos la recíproca posición de la lógica y la mecánica. (Se podría construir la malla con figuras de diferentes clases; por ejemplo, con triángulos y hexágonos.) Que una figura como la arriba citada se pueda describir por una malla de una forma dada no dice nada sobre la figura misma. (Pues esto es válido para todas las figuras de esta clase.) Pero aquello que caracteriza a la figura-es el hecho de que se la pueda describir completamente con una determinada malla de determinada finura.
Así, pues, nada dice acerca del universo que se le pueda describir por la mecánica newtoniana; pero sí dice algo que se le pueda describir así como de hecho se le describe. Y también dice algo sobre el mundo que se le pueda describir más sencillamente por una mecánica que por otra.
- 6.343 La mecánica es un intento de construir según un plan único todas las proposiciones verdaderas que se necesitan para la descripción del mundo.
- 6.3431 A través de su completo aparato lógico, las leyes físicas hablan aún de los objetos del mundo.
- 6.3432 No debemos olvidar que la descripción del mundo por la mecánica es siempre completamente general. No se habla nunca de puntos materiales determinados, sino sólo de algunos puntos cualesquiera.
6.35 Por cuanto en nuestra figura las manchas son figuras geométricas, la geometría no puede evidentemente decir nada sobre su forma y posición efectivas. Pero la malla es puramente geométrica, y todas sus propiedades pueden darse a priori.
Leyes como el principio de razón, etc., tratan de la malla y no de lo que la malla describe.
- 6.36 Si hubiese una ley de causalidad, podría decir se así: «Hay leyes naturales.» Pero no se puede, naturalmente, decir: se muestra.
- 6.361 En la terminología de Hertz se podría decir: Sólo conexiones regulares son pensables.
6.3611 No se puede comparar un proceso con el «transcurso del tiempo» -tal cosa no existe-, sino sólo con otro proceso (tal que la marcha del cronómetro).
Por lo tanto, la descripción del proceso temporal sólo es posible en cuanto lo refiramos a otro proceso.
Esto es exactamente análogo para el espacio. Cuando, por ejemplo, se dice que de dos acontecimientos que se excluyen recíprocamente ninguno de los dos puede ocurrir, porque no hay ninguna causa, por la cual deba ocurrir uno mejor que el otro. En realidad, somos incapaces de describir uno de los dos acontecimientos si no se da una cierta clase de asimetría. Y si hay tal asimetría, podemos considerarla como la causa del acontecer del uno y del no acontecer del otro.
6.36111 El problema kantiano de la mano derecha y de la mano izquierda, que no se puede hacer que coincidan superponiéndolas, se da ya en el plano, aunque siempre en el espacio unidimensional, en el que dos figuras congruentes, a y b, no pueden coincidir sin sacarlas fuera de su espacio,
La mano derecha y la izquierda son en realidad completamente congruentes, y el hecho de que no se puedan hacer coincidir no tiene nada que ver con ello.
Se podría meter el guante derecho en la mano izquierda si fuese posible darle la vuelta en un espacio cuatridimensíonal.
- 6.362 Lo que se puede describir también puede ocurrir, y lo que está excluido por la ley de la causalidad no puede describirse.
- 6.363 El proceso de inducción consiste en admitir la ley más simple que pueda armonizarse con nuestra experiencia.
6.3631 Este proceso, pues, no tiene fundamentación lógica, sino sólo psicológica.
Es claro que no hay ningún fundamento para creer que realmente acontezca el acontecimiento más simple.
- 6.36311 Que el sol amanezca mañana es una hipótesis: y esto significa que no sabemos si amanecerá.
- 6.37 No existe la necesidad de que una cosa deba acontecer porque otra haya acontecido; hay sólo una necesidad lógica.
- 6.371 A la base de toda la moderna concepción del mundo está la ilusión de que las llamadas leyes naturales sean la explicación de los fenómenos naturales.
- 6.372 Así, los modernos confían en las leyes naturales como en algo inviolable, lo mismo que los antiguos en Dios y en el destino. Y ambos tienen razón y no la tienen; pero los antiguos eran aún más claros, en cuanto reconocían un limite preciso, mientras que el sistema moderno quiere aparentar que todo está explicado.
- 6.373 El mundo es independiente de mi voluntad.
- 6.374 Aunque todo lo que deseáramos ocurriese, esto sería solamente, por así decirlo, una merced de la suerte, pues no hay conexión lógica entre voluntad y mundo que pueda garantizar tal cosa, ni nosotros podríamos a su vez querer esta supuesta conexión física.
- 6.375 Lo mismo que sólo hay una necesidad lógica, así sólo hay una imposibilidad lógica.
6.3751 Que dos colores, por ejemplo, se encuentren simultáneamente en un punto del campo visual, es imposible, lógicamente imposible, porque lo excluye la estructura lógica del color.
Consideremos cómo se presenta esta contradicción en física. Más o menos como sigue: Una partícula no puede tener dos velocidades al mismo tiempo; es decir, que no puede al mismo tiempo estar en dos sitios; es decir, que partículas en diferentes lugares y al mismo tiempo no pueden ser idénticas.
(Es claro que el producto lógico de dos proposiciones elementales no puede ser ni una tautología ni una contradicción. La afirmación de que un punto del campo visual tenga dos colores diferentes al mismo tiempo es una contradicción.)
- 6.4 Todas las proposiciones tienen igual valor.
6.41 El sentido del mundo debe quedar fuera del mundo. En el mundo todo es como es y sucede como sucede: en él no hay ningún valor, y aunque lo hubiese no tendría ningún valor.
Si hay un valor que tenga valor, debe quedar fuera de todo lo que ocurre y de todo ser-así. Pues todo lo que ocurre y todo ser-así son casuales.
Lo que lo hace no casual no puede quedar en el mundo, pues de otro modo sería a su vez casual.
Debe quedar fuera del mundo.
6.42 Por lo tanto, puede haber proposiciones de ética.
Las proposiciones no pueden expresar nada más alto.
6.421 Es claro que la ética no se puede expresar.
La ética es trascendental.
(Ética y estética son lo mismo.)
6.422 El primer pensamiento que surge cuando se propone una ley ética de la forma «tú debes», es: ¿y qué si no lo hago? Pero es claro que la ética no se refiere al castigo o al premio en el sentido común de los términos.
Así, pues, la cuestión acerca de las consecuencias de una acción debe ser irrelevante. Al menos, estas consecuencias, no pueden ser acontecimientos. Pues debe haber algo justo en la formulación de la cuestión. Sí que debe haber una especie de premio y de castigo ético, pero deben encontrarse en la acción misma.
(Y esto es también claro, que el premio debe ser algo agradable y el castigo algo desagradable.)
- 6.423 De la voluntad como sujeto de la ética no se puede hablar. Y la voluntad como fenómeno solo interesa a la psicología.
6.43 Si la voluntad, buena o mala, cambia el mundo, sólo puede cambiar los límites del mundo, no los hechos. No aquello que puede expresarse con el lenguaje.
En resumen, de este modo el mundo se convierte, completamente, en otro. Debe, por así decirlo, crecer o decrecer como un todo.
El mundo de los felices es distinto del mundo de los infelices.
- 6.431 Así, pues, en la muerte el mundo no cambia, sino cesa.
6.4311 La muerte no es ningún acontecimiento de la vida.
La muerte no se vive.
Si por eternidad se entiende no una duración temporal infinita, sino la intemporalidad, entonces vive eternamente quien vive en el presente. Nuestra vida es tan infinita como ilimitado nuestro campo visual.
6.4312 La inmortalidad temporal del alma humana, esto es, su eterno sobrevivir aun después de la muerte, no solo no está garantizada de ningún modo, sino que tal suposición no nos proporciona en principio lo que merced a ella se ha deseado siempre conseguir. ¿Se resuelve quizás un enigma por el hecho de yo sobreviva eternamente? Y esta vida eterna ¿no es tan enigmática como la presente? La solución del enigma de la vida en el espacio y en el tiempo está fuera del espacio y del tiempo.
(No son los problemas de la ciencia natural los que hemos de resolver aquí.)
- 6.432 Cómo sea el mundo, es completamente indiferente para lo que está más alto. Dios no se revela en el mundo.
- 6.4321 Los hechos pertenecen todos sólo al problema, no a la solución.
- 6.44 No es lo místico como sea el mundo, sino que sea el mundo.
6.45 La visión del mundo sub specie aeterni es su contemplación como un todo –limitado-.
Sentir el mundo como un todo limitado es lo místico.
6.5 Para una respuesta que no se puede expresar, la pregunta tampoco puede expresarse.
No hay enigma.
Si se puede plantear una cuestión, también se puede responder.
6.51 El escepticismo no es irrefutable, sino claramente sin sentido si pretende dudar allí en donde no se puede plantear una pregunta.
Pues la duda sólo puede existir cuando hay una pregunta; una pregunta, sólo cuando hay una respuesta, y ésta únicamente cuando se puede decir algo.
- 6.52 Nosotros sentimos que incluso si todas las posibles cuestiones científicas pudieran responderse, el problema de nuestra vida no habría sido más penetrado. Desde luego que no queda ya ninguna pregunta, y precisamente ésta es la respuesta.
6.521 La solución del problema de la vida está en la desaparición de este problema.
(¿No es ésta la razón de que los hombres que han llegado a ver claro el sentido de la vida después de mucho dudar, no sepan decir en qué consiste este sentido?)
- 6.522 Hay, ciertamente, lo inexpresable, lo que se muestra a si mismo; esto es lo místico.
- 6.53 El verdadero método de la filosofía sería propiamente éste: no decir nada, sino aquello que se puede decir; es decir, las proposiciones de la ciencia natural –algo, pues, que no tiene nada que ver con la filosofía-; y siempre que alguien quisiera decir algo de carácter metafísico, demostrarle que no ha dado significado a ciertos signos en sus proposiciones. Este método dejaría descontentos a los demás – pues no tendrían el sentimiento de que estábamos enseñándoles filosofía-, pero sería el único estrictamente correcto.
6.54 Mis proposiciones son esclarecedoras de este modo; que quien me comprende acaba por reconocer que carecen de sentido, siempre que el que comprenda haya salido a través de ellas fuera de ellas. (Debe, pues, por así decirlo, tirar la escalera después de haber subido.)
Debe superar estas proposiciones; entonces tiene la justa visión del mundo.
 7 De lo que no se puede hablar, mejor es callarse.
7 De lo que no se puede hablar, mejor es callarse.